- #1
dynamicskillingme
- 27
- 0
Homework Statement
Homework Equations
L = T-V
The Attempt at a Solution
I got a forumla for the lagrangian as
check the L written above and set up the Lagrange's equations of motion...dynamicskillingme said:I got a forumla for the lagrangian as

Its more I don't know if the L is correct and wanted to check what the derivation is with someone else's because I'm pretty sure my derivation is wrong.drvrm said:check the L written above and set up the Lagrange's equations of motion...
dynamicskillingme said:Its more I don't know if the L is correct and wanted to check what the derivation is with someone else's because I'm pretty sure my derivation is wrong.
dynamicskillingme said:Its more I don't know if the L is correct and wanted to check what the derivation is with someone else's because I'm pretty sure my derivation is wrong.
You have neglected the rotational inertia of the spheres about their centers. This will add additional terms to T. Also, check the sign of the gravitational potential energy part of L.dynamicskillingme said:Its more I don't know if the L is correct and wanted to check what the derivation is with someone else's because I'm pretty sure my derivation is wrong.
Each ball does rotate as either ##\theta## or ##\psi## changes. Consider a ball attached to the end of a stick as shown in the figure below. As the stick rotates through an angle θ, the ball also rotates through θ.dynamicskillingme said:I don't believe the balls are allowed to rotate about their centers.
The potential energy is subtracted in the Lagrangian: L = T - V. You got the sign correct for the spring potential energy.Why wouldn't the gravitational potential be positive?
It's just a kinetic energy term due to rotation about the center of mass.dynamicskillingme said:Yeah I agree with that, but what other term would that introduce?
If θ increases, both the spring potential energy and the gravitational potential energy increase.Also wouldn't the gravity term be the opposite direction to the spring?
dynamicskillingme said:Could you possibly write out the correct Lagrangian as I feel like I'm stumbling around it and would love to inspect the correct one. And sorry there is a note at the start of my work I forgot and it just says
That's getting very close to the correct ##L##. However, you need to include a rotational KE term associated with ##\dot{\theta}## as well as with ##\dot{\psi}##. And, as you say, the coefficient for the gravity terms needs to be corrected.dynamicskillingme said: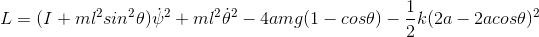
When evaluating ##\frac{\partial{L}}{\partial \theta}##, how did you get factors of ##\dot{\theta}## to appear?
This expression for ##L## looks correct to me as long as the distance ##l## has the correct interpretation.dynamicskillingme said: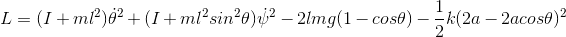
The Lagrangian of a centrifugal regulator is a mathematical function that represents the total energy of the system, taking into account the potential and kinetic energies. It is used to describe the motion of the regulator and its components.
The Lagrangian of a centrifugal regulator is derived using the Lagrangian mechanics approach, which is based on the principle of least action. This means that the path taken by the regulator is the one that minimizes the action, which is the integral of the Lagrangian over time.
The Lagrangian of a centrifugal regulator is made up of two parts: the kinetic energy term, which is the energy due to the motion of the regulator and its components, and the potential energy term, which is the energy due to the position of the regulator in a gravitational or centrifugal field.
The Lagrangian of a centrifugal regulator is used in engineering applications to model the behavior of the regulator and optimize its design. It can also be used to analyze the stability and control of the regulator in different operating conditions.
Yes, the Lagrangian of a centrifugal regulator can be used to solve real-life problems in engineering and physics. It provides a mathematical framework for analyzing and predicting the behavior of the regulator in various scenarios, making it a valuable tool in designing and improving centrifugal regulators.