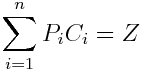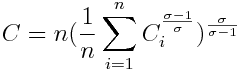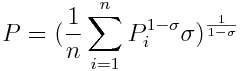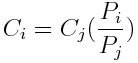- #1
Boardish
- 1
- 0
Hello there! It's my first time posting here, I hope you guys will be good to me :).
I took a one year break to study a language abroad, and now it seems like I forgot everything math-wise. I'm preparing for a test and I'm having a really hard time doing the following problem.
I need to maximize the utility of a consumer with obviously a constraint.
https://www.physicsforums.com/attachments/3396._xfImport
https://www.physicsforums.com/attachments/3397._xfImport
https://www.physicsforums.com/attachments/3395._xfImport
Where C is the aggregate consumption, P the aggregate price and Z the level of expenditure.
I need to maximize the utility function (the consumption) C for the level of expenditure Z.
I also need to show with the first order conditions that
https://www.physicsforums.com/attachments/3398._xfImport
I found a somewhat similar question (http://mathhelpboards.com/calculus-10/lagrange-multipliers-summation-function-constraint-3821.html) but I have a hard time working with the exponents and the summation.
Thanks a lot!
EDIT : Or if someone can only explain to me how I actually derive the summation
https://www.physicsforums.com/attachments/3396._xfImport
I'll try to figure everything else :)
I took a one year break to study a language abroad, and now it seems like I forgot everything math-wise. I'm preparing for a test and I'm having a really hard time doing the following problem.
I need to maximize the utility of a consumer with obviously a constraint.
https://www.physicsforums.com/attachments/3396._xfImport
https://www.physicsforums.com/attachments/3397._xfImport
https://www.physicsforums.com/attachments/3395._xfImport
Where C is the aggregate consumption, P the aggregate price and Z the level of expenditure.
I need to maximize the utility function (the consumption) C for the level of expenditure Z.
I also need to show with the first order conditions that
https://www.physicsforums.com/attachments/3398._xfImport
I found a somewhat similar question (http://mathhelpboards.com/calculus-10/lagrange-multipliers-summation-function-constraint-3821.html) but I have a hard time working with the exponents and the summation.
Thanks a lot!
EDIT : Or if someone can only explain to me how I actually derive the summation
https://www.physicsforums.com/attachments/3396._xfImport
I'll try to figure everything else :)
Attachments
Last edited: