mbond
- 41
- 7
The number of visible galaxies is to vanish in the long-term future with the ##\Lambda##CDM model (book and papers of L. Krauss et al). I am interested in a quantitative study on how the population of galaxies decreases; I could not find one so I do it myself:
The scale factor: ##\displaystyle\frac{a(t)}{a_0}=(\frac{\Omega_{m0}}{\Omega_{\Lambda0}})^{^{^{1/3}}}\sinh^{^{2/3}}(\frac{t}{t_{\Lambda}})## with ##t_\Lambda=\displaystyle\frac{2}{\sqrt{3\Lambda c^2}}##, ##\Omega_x## the densities, and ##\Lambda## the cosmological constant.
The density of matter: ##\Omega_m(a)=\displaystyle\frac{\Omega_{m0}}{\Omega_{m0}+\Omega_{rad0}(a/a_0)^{-1}+\Omega_{\Lambda0}(a/a_0)^3}##
The particle horizon: ##d_p(t)=a(t)\displaystyle\int_{0}^{t}\frac{cdt^\prime}{a(t^\prime)}##
The event horizon: ##d_E(t)=a(t)\displaystyle\int_{t}^{\infty}\frac{cdt^\prime}{a(t^\prime)}##
These horizons are shown in the figure:
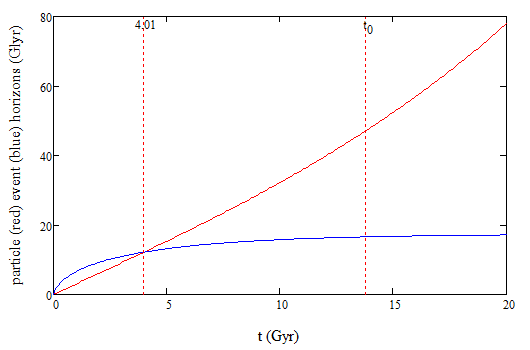
The two horizons cross at t=4.01 Gyr.
Let be ##h(t)## the smallest of the two horizons: ##h(t)=\min(d_p(t),d_E(t))##. The number of visible galaxies is then: ##V(t)\sim \Omega_m(a(t))h(t)^3## and this is shown on the figure below:
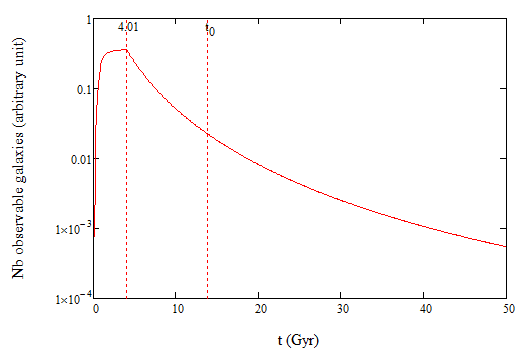
The number of visible galaxies was maximum at 4.1 Gyr when the two horizons cross. Today it has decreased by a factor of 16, and at t=37.2 Gyr, it will have diminished by another factor of 16.
Is my calculation correct?
The scale factor: ##\displaystyle\frac{a(t)}{a_0}=(\frac{\Omega_{m0}}{\Omega_{\Lambda0}})^{^{^{1/3}}}\sinh^{^{2/3}}(\frac{t}{t_{\Lambda}})## with ##t_\Lambda=\displaystyle\frac{2}{\sqrt{3\Lambda c^2}}##, ##\Omega_x## the densities, and ##\Lambda## the cosmological constant.
The density of matter: ##\Omega_m(a)=\displaystyle\frac{\Omega_{m0}}{\Omega_{m0}+\Omega_{rad0}(a/a_0)^{-1}+\Omega_{\Lambda0}(a/a_0)^3}##
The particle horizon: ##d_p(t)=a(t)\displaystyle\int_{0}^{t}\frac{cdt^\prime}{a(t^\prime)}##
The event horizon: ##d_E(t)=a(t)\displaystyle\int_{t}^{\infty}\frac{cdt^\prime}{a(t^\prime)}##
These horizons are shown in the figure:
The two horizons cross at t=4.01 Gyr.
Let be ##h(t)## the smallest of the two horizons: ##h(t)=\min(d_p(t),d_E(t))##. The number of visible galaxies is then: ##V(t)\sim \Omega_m(a(t))h(t)^3## and this is shown on the figure below:
The number of visible galaxies was maximum at 4.1 Gyr when the two horizons cross. Today it has decreased by a factor of 16, and at t=37.2 Gyr, it will have diminished by another factor of 16.
Is my calculation correct?