- #1
baby_1
- 159
- 15
Hello
as you see this example and solution
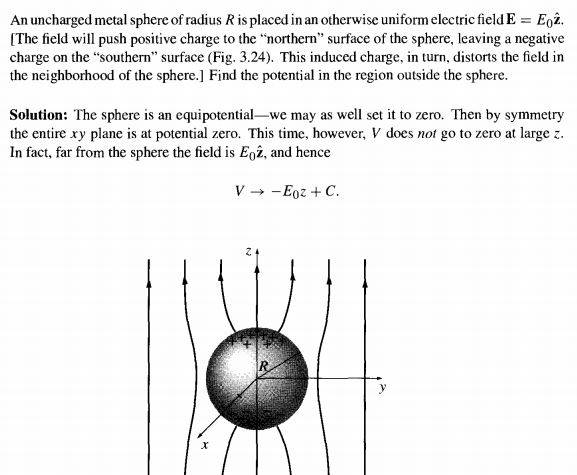
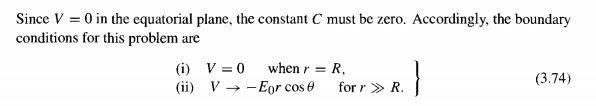
if we assume the R of conductor sphere is 5m and check voltage in different z we obtain(for example z=1m and z=2)
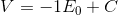
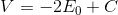
and as we know in conductor we doesn't have voltage differences so this equation should be the same
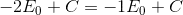
C=0
but voltage aren't the same
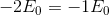
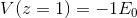
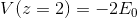
why in the conductor sphere voltages aren't the same? or i do mistake to understand this example
as you see this example and solution
if we assume the R of conductor sphere is 5m and check voltage in different z we obtain(for example z=1m and z=2)
and as we know in conductor we doesn't have voltage differences so this equation should be the same
C=0
but voltage aren't the same
why in the conductor sphere voltages aren't the same? or i do mistake to understand this example