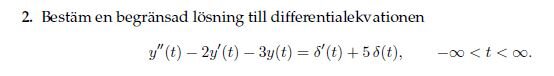MHB Laplace / inverse laplace transform

Click For Summary
The discussion centers on the application of the Laplace transform to solve a differential equation with delta functions on the right-hand side. The transformation of the expression $$\frac{-1}{s+1} + \frac{2}{s-3}$$ does not yield the expected result of $$-e^{-t} + 2e^{3t}$$ due to the presence of delta functions, which require the use of step functions to account for their effects at specific values of x. Participants clarify that the delta functions indicate discontinuities, necessitating the inclusion of Heaviside step functions to properly define the solution for t greater than certain thresholds. The discussion highlights the importance of understanding the implications of delta functions and their derivatives in the context of Laplace transforms. Overall, the conversation emphasizes the need to incorporate step functions when dealing with differential equations influenced by delta functions.
goohu
Messages
53
Reaction score
3
View attachment 9453

Problem: Find a (limited?) solution to the diff eq.

View attachment 9454
At the end of the solution, when you transform $$\frac{-1}{s+1} + \frac{2}{s-3}$$
why doesn't it become $$-e^{-t} + 2e^{3t} $$, t>0 ?
 

Attachments

  • prob.JPG
    prob.JPG
    6 KB · Views: 174
  • Sol.JPG
    Sol.JPG
    11.9 KB · Views: 164
Physics news on Phys.org
That would be correct if the right hand side of the equation were 0. But the delta functions on the right mean that those are correct only for x greater than certain values so the step functions are needed.
 
What values are those and how are the step functions used?
 
Do you know what "\delta(x)" and "\delta'(x)" mean?
 

Similar threads

Undergrad Laplace transform of a simple equation (Simple question)
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Understanding the Laplace Transform of cos(t)/t
  • · Replies 7 ·
Replies
7
Views
6K
Undergrad On Laplace transform of derivative
  • · Replies 17 ·
Replies
17
Views
3K
Undergrad On a bijective Laplace transform
  • · Replies 1 ·
Replies
1
Views
3K
Undergrad Laplace transform linearity problem
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Inverse Laplace transform of a piecewise defined function
  • · Replies 5 ·
Replies
5
Views
5K
Undergrad Solving PDE with Laplace Transforms & Inverse Lookup
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Solution of delayed forcing function
  • · Replies 5 ·
Replies
5
Views
3K
What is the Inverse Laplace Transform of e^(-sx^2/2)?
  • · Replies 10 ·
Replies
10
Views
2K
Inverse Laplace Transform of a product of exponential functions
  • · Replies 1 ·
Replies
1
Views
4K