Laplace transform of proper rational function

[member 731016]

Homework Statement

Please see below

Relevant Equations

$\frac{2s + 1}{((s - 1)(s - 1)} = \frac{A(s - 1) + B(s - 1)}{(s - 1)(s - 1)}$

For this problem (b),

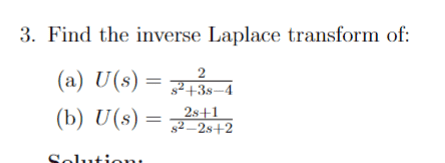
The solution is,

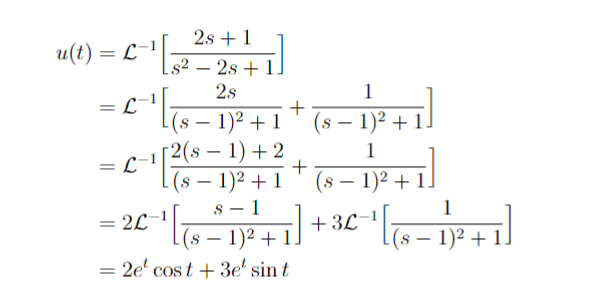
However, I don't understand how they got their partial fractions here (Going from step 1 to 2).

My attempt to convert into partial fractions is:

$\frac{2s + 1}{(s - 1)(s - 1)} = \frac{A(s - 1) + B(s - 1)}{(s - 1)(s - 1)}$

Thus,

$2s + 1 = A(s - 1) + B(s - 1)$
$2s + 1 = (A + B)s - A - B$

$2 = A + B$
$1 = - A - B$
$-1 = A + B$

However, $2 ≠ -1$

Does someone please know how they got their partial fractions expression in step 2?

Thanks!

 

[FactChecker]

I disagree with their first step. $\frac {2s+1}{s^2-2s+1} = \frac {2s}{(s-1)^2} + \frac{1}{(s-1)^2}$.
I don't know why they are adding 1 to the denominators.
CORRECTION: The text in the OP is a typo and the actual problem has denominator $s^2-2s+2$. Thanks, @Orodruin .

 

[Orodruin]

I disagree with their first step. $\frac {2s+1}{s^2-2s+1} = \frac {2s}{(s-1)^2} + \frac{1}{(s-1)^2}$.
I don't know why they are adding 1 to the denominators.

Because the actual problem has the denominator $s^2 - 2s + \color{Red}{2}$ … the 1 in the solution’s first expression is a typo.

 

[Orodruin]

Apart from that, your partial fraction ansatz is equivalent to assuming
$$
2s + 1 = (A+B)(s-1)
$$
This obviously will not work. You should check how to do partial fractions when the denominator is a square (or higher power). Even if it will not be useful here.

 

[Orodruin]

is a typo

Typos seem quite overabundant in the solutions of the OP’s threads. If this is the main mode of learning, they may want to consider a different source.

 

[FactChecker]

There are no tricky partial fractions involved in this problem. Every step is a simple rearrangement of the fractions.

 

[Orodruin]

I mean, you can do partial fractions, but the roots of the denominator are complex and the approach in the solution is much more straightforward.