Laplace Transform problem

[Chris L T521]

Thanks again to those who participated in last week's POTW! Here's this week's problem!

-----

Problem: Let $\mathcal{L}\{g(t)\}$ denote the Laplace transform of $g(t)$. Show that
\[\mathcal{L}\left\{\left\lfloor \frac{t}{a} \right\rfloor\right\} = \frac{e^{-as}}{s(1-e^{-as})}\]
where $a>0$ and $\lfloor x\rfloor$ denotes the floor function (i.e. the greatest integer less than or equal to $x$).

-----

Hint: [sp]Express $\left\lfloor \dfrac{t}{a}\right\rfloor$ as a difference between a continuous function and an $a$-periodic function, then take the Laplace transform of the result.

The following formula will come in handy when taking the Laplace transform of the periodic function: If $f(t)$ is piecewise continuous and $p$-periodic, and $f_p(t)$ denotes one period of $f(t)$, then

\[\mathcal{L}\{f(t)\} = \frac{1}{1-e^{-as}}\int_0^p e^{-st}f_p(t)\,dt = \frac{\mathcal{L}\{f_p(t)\}}{1-e^{-as}}\]

---

Can't figure out the correct functions to use? It's alright...click the next spoiler to find out what I'm looking for!

[sp]The proper way to express $\left\lfloor \dfrac{t}{a}\right\rfloor$ would be as follows:
\[\left\lfloor \frac{t}{a} \right\rfloor = \frac{t}{a} - f(t)\]
where $f(t)$ is the $a$-periodic sawtooth function pictured below.

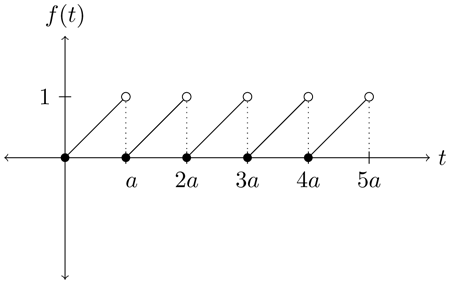Note that one period of this function is given by $f_a(t) = \dfrac{t}{a}(u(t)-u(t-a))$ where
\[u(t)=\begin{cases}1 & t\geq 0\\ 0 & t<0\end{cases}\] is the Heaveside step function.[/sp][/sp]

 

[Chris L T521]

No one answered this week's problem. You can find my solution below.

[sp]Consider the sawtooth wave of period $a$. Let us define one period of this function by $f_a(t) = \dfrac{t}{a}(u(t) - u(t-a))$ (several periods of $f(t)$ are shown below).

We now can define $\left\lfloor\dfrac{t}{a}\right\rfloor = \dfrac{t}{a} - f(t)$ for any $t\geq 0$.

Therefore, $$\mathcal{L}\left\{\left\lfloor \frac{t}{a}\right\rfloor\right\} = \mathcal{L}\left\{\frac{t}{a}\right\} - \mathcal{L}\{f(t)\} = \frac{1}{as^2} - \mathcal{L}\{f(t)\}.$$

To compute the Laplace transform of $f(t)$, you'll need to recall the Laplace transform formula for periodic functions; that is, if $g(t)$ is piecewise continuous for $t\geq 0$ and is $p$-periodic, then
$$\mathcal{L}\{g(t)\} = \frac{1}{1-e^{-ps}}\mathcal{L}\{g_p(t)\} = \frac{1}{1-e^{-ps}}\int_0^p e^{-st}g_p(t)\,dt$$
where, again, $g_p(t)$ is one period of $g(t)$. To help us compute $\mathcal{L}\{f_a(t)\}$, let us also recall the derivative formula $\mathcal{L}\{tf_a(t)\} = -\dfrac{d}{ds}\mathcal{L}\{f_a(t)\}$.

We now see that

$$\begin{aligned} \mathcal{L}\{f_a(t)\} &= \frac{1}{a}\mathcal{L}\{t(u(t) - u(t-a))\} \\ &= -\frac{1}{a}\frac{d}{ds}\left[\mathcal{L}\{u(t)\} - \mathcal{L}\{u(t-a)\}\right]\\ &= -\frac{1}{a}\frac{d}{ds}\left(\frac{1}{s} - \frac{e^{-as}}{s}\right)\\ &= -\frac{1}{a}\left(-\frac{1}{s^2} - \frac{-ase^{-as} - e^{-as}}{s^2}\right)\\ &= \frac{1-e^{-as}-ase^{-as}}{as^2}\end{aligned}$$

Thus,

$$\mathcal{L}\{f(t)\} = \frac{1}{1-e^{-as}} \mathcal{L}\{f_a(t)\} = \frac{1-e^{-as}-ase^{-as}}{as^2(1-e^{-as})}$$

and therefore, we have that

$$\mathcal{L}\left\{\left\lfloor\frac{t}{a} \right\rfloor\right\} = \mathcal{L}\left\{\frac{t}{a}\right\} - \mathcal{L}\{f(t)\} = \frac{1}{as^2} - \frac{1-e^{-as}-ase^{-as}}{as^2(1-e^{-as})} = \frac{e^{-as}}{s(1-e^{-as})}.$$[/sp]