- #1
sergiokapone
- 302
- 17
Hi all, I interested in how can I get low of motion in for orbiting particle in a uniform magnetic field
$$\frac{d\vec{r}}{dt} = \vec{\omega}\times\vec{r},\qquad
\vec{\omega} = \frac{e\vec{B}}{mc},$$
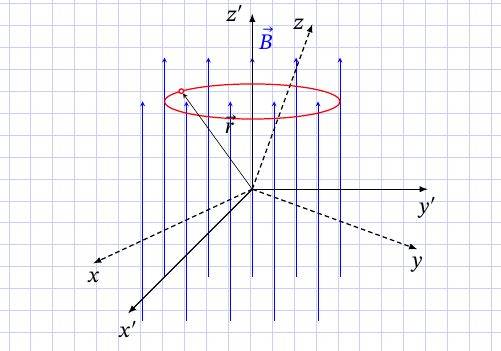
Of course, rotating about z' axis is very simple.
\begin{equation}\label{eq:K}
\begin{cases}
x' = R\cos(\omega_{z'} t ), \\
y' = R\sin(\omega_{z'} t ), \\
z' = z'_0.
\end{cases}
\end{equation}
But what can I do, when axes is arbitrary oriented?
$$\frac{d\vec{r}}{dt} = \vec{\omega}\times\vec{r},\qquad
\vec{\omega} = \frac{e\vec{B}}{mc},$$
Of course, rotating about z' axis is very simple.
\begin{equation}\label{eq:K}
\begin{cases}
x' = R\cos(\omega_{z'} t ), \\
y' = R\sin(\omega_{z'} t ), \\
z' = z'_0.
\end{cases}
\end{equation}
But what can I do, when axes is arbitrary oriented?
Last edited: