Least-squares calculation with a pinch of weights and monte-carlo

[imsolost]

Hello all,
I am a bit lost with a problem and my reasoning and would like to hear your thoughts about it.
Problem is the following :

For a set of data y_i, I need to find the best value for A_m given :

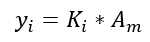
"i" is an indice {1, 2, 3, ... up to something like 20}. "m" stands for "mass" (Am is a physical quantity named "mass activity").

Anyway, so I thought about using common least-square method...

The data y_i is not a set of "exact" values though... It comes from a report from a laboratory and they give me a set of values, each with an associated standard deviation uncertainty. For some y_i, value seems to be accurately measured since the standard deviation is small, while sometimes, for other values, it can be bit bigger.

So I thought about using weighted least-square method...

As i understand weighted LS, I write :

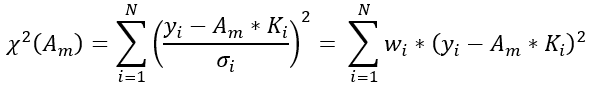
I force the condition :

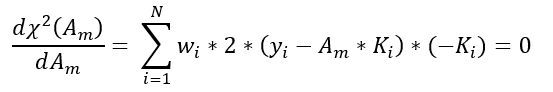
And thus Am should look like :

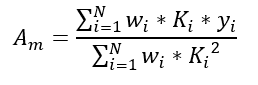
where Wi=1/sigma²_i are the weights. So far, so good.

Now, here is the tricky part... K_i also is "uncertain" : K_i comes from an big expression containing 3 uncertain parameters : λ₁, λ₂, λ₃. These λ₁, λ₂, λ₃ are calculated from other datas with non-linear expressions, and I had to propagate the uncertainties on these datas using Monte-Carlo methods. So what I have is something like 1000 "sets" of slightly different λ₁, λ₂, λ₃. I use these 1000 sets and my big K_i expression to generate a set of 1000 K_i.

So, the question becomes :
1) Should I use my WLS expression to calculate A_m for each of the 1000 K_i, which would give me 1000 slightly different A_m (and then i can happily get the mean, standard deviation or whatever on these 1000 A_m values and I'm done).

2) Or should i use a regular LS expression (i.e. without weights) and handle the uncertainty on the y_i with Monte-Carlo. So i mean getting something like 1000 random normally-distributed sampling around the y_i's and given the associated standard deviation uncertainty from the laboratory. Then with 1000 set of y_i, my previous 1000 set of K_i and the common LS formula, i would get 1000 slightly different A_m (and then i can happily get the mean, standard deviation or whatever on these 1000 A_m values and I'm done)

3) Or should I do both 1) AND 2), i.e. doing "2)" but using the WLS instead of the LS formula ?

At the time of writing this, I'm doing "3)" but i wonder if this is not a bit stupid. Am I accounting for these uncertainties twice and over-estimating the uncertainty on A_m ?

Sorry if the post is a bit long but i really tried to explain the thing as detailed as possible. Also sorry if the question is a bit dumb/obvious but I think i thought about this problem a bit too much and i feel like my brain is totally biased / unable to think about this stuff anymore :D

Anyway, big thank you for your time !

 

[Stephen Tashi]

The data y_i is not a set of "exact" values though...

Now, here is the tricky part... K_i also is "uncertain"

I suggest you use total least squares regression https://en.wikipedia.org/wiki/Total_least_squares

However, the question of "what's the optimal procedure" is subjective unless you can quantify the cost or utility of results. For example, in ordinary least squares regression, we take for granted that the sum of the squared differences between predicted y-vales and the data is the "cost" of the resulting fit. Mathematics then tells us how to minimize this cost, but it doesn't justify using this cost as a measure of how "good" the fit is. The choice of how to measure the "goodness" of a fit is subjective.

If your eventual goal is to publish a result in a journal, it's advisable to see what methods other published papers used. That will show which subjective choices are backed by custom and tradition.

(When I click on the attachment, I only see a title.)

 

[imsolost]

I do agree about what you say about "goodness" of the fit, and indeed as u guessed, this is a study that will be published so i need to make sure people will "adhere" to it. And i haven't find a paper where people faced the same thing.

I already saw about "total" least square but i have no idea how to use it considering that the information about the uncertainty on K_i is "contained" in the 1000 samplings on K_i and I have the feeling this is the only way i can decently propagate the uncertainty of the λ's. So i have this (wrong?) feeling that i have to use Monte Carlo again...