- #1
woundedtiger4
- 188
- 0
can anyone please show me that how to apply Lebesgue integral by showing some example like we do Riemann integral in calculus class? for example:
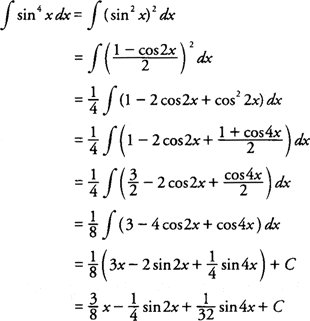
thanks a tonneCongruent said:It is a standard fact that if f is a real valued function defined on a closed interval which is integrable in the Riemann sense, then the function is measurable and integrable (in the Lebesgue sense) and the two integrals are equal. So if what you're asking for is an example of finding an anti-derivative of functions as is done in calculus, then the procedure is to note the above and integrate.
However, the power and utility of the Lebesgue integral is the ease with which more complicated functions can be integrated (the integral can easily be broken up over various sets which have specific properties and has powerful convergence theorems; there also exist functions which may fail to be integrable in the Riemann sense; see the characteristic function of the rationale over any closed interval). But these don't have general calculus style approaches. These sorts of integration arguments require more care than applying a set of procedural formulas.
Bacle2 said:Sorry for the necropost; I ran into this in a search. Feel free to Ignore if you don't need
it anymore:
Just like the case with a Riemann integral, where you do Riemann sums, in the Lebesgue case, you do Lebesgue sums, where you partition the range instead of the domain, and then the value of the Lebesgue integral is the sum of these values:
If your range likes in [y1,y2], then you partition your range, select some points yi, i.e., you select a point in each interval of the range ---remember you select points in your domain when you do Riemann sums--then your sums are of the form:
Ʃy=1n yi*m(A)
where A is the preimage set under f, so that you sum a value selected in your range. There are , of course, conditions for this integral to exist/converge; some of these conditions can be described with simple functions, but I think it is important to note that, just like with Riemann, the value of the sum should approach a limit as the number of partitions increases.
Is that what you were asking?
times the measure of the associated preimage.
woundedtiger4 said:Edited note: what is m here? is it some function? if it takes A (which is domain) then what does map into ? range? can you please guide me in the context of probability if it's possible. Thanks
Bacle2 said:In a very basic and informal way, this is part of how it is laid out:
You have a measure triple (X, m, Sigma). X is a set/space, m is a measure (see below), and the sigma algebra is a collection of subsets of X.
You have a measure m, which is a function defined on a certain collection of subsets that is countably subadditive (measure of the union of sets is ≤ sum of the measures), non-negative and monotone (A Subset B, then m(A) < m(B)) .
You normalize your space, so that m(X)=1 . Then the probability of an event is its measure. So that, for example, the probability of hitting a rational with a dart thrown
at random is the measure of the subset of rationals in X . In the Lebesgue measure , the
measure of all rationals is 0 .
I need to go, but let me know if there is something else that interests you.
woundedtiger4 said:so m in lebesgue gives the width of rectangle as it gives in reimann?
I am lil' confused that, is m=f^-1 (E) ?
Bacle2 said:m is a function that is intended to abstract/generalize the properties you would want
to find in the measure of a set. So, the Lebesgue measure of an interval is its length,
and, with some adjustments, the measure of a rectangle is the product of the lengths
of the intervals forming the sides of the rectangle.
f^-1(E) is just the set {x: f(x) is in E}. What you do is you break down your range
--like the way you break down your domain -- as {y1, y2,...,yn} , and --again,like
the case of the Riemann integral-- you select one point yi* in each interval [yi,yi+1)
and then you consider the measure of the preimage.The Lebesgue integral is then
the sum yi*m(Ei). There are rules for the (net ) convergence of the Lebesgue
integral: the Leb integral equals, 'L' if,given any e>0 , there must be some del.>0 with
||P||< del. implies the integral of any of these partitions is within less than e of L,
i.e. | Int f -L| <e when ||P||< del.
Along the lines of what Pwsnafu said, you define the Lebesgue measure (in R
here, since you want to do probability; you can define measures in general topological
space) by defining
declaring the length of an interval (a,b) to be b-a and then defining the measure of a
subset of R to be the infimum of the measures over all covers of a set.
pwsnafu said:One thing you will be surprised with: it is possible to construct a definition of integral which is equivalent to the Lebesgue integral on ℝ, but nonetheless partitions the domain. It's called the McShane integral, but you'll want to read about the Henstock-Kurzweil integral first.
woundedtiger4 said:WOW, how many integrals are out in the world?There's an infinite number. The Riemann integral, McShane integral and Henstock-Kurzweil integral are all the same in the sense they are all Riemann sums. The trick is changing which partitions you allow. If you allow lots, you need to restrict f to guarantee the limit existing (Riemann). If you restrict the partitions you can weaken f (H-K). McShane (and hence Lebesgue) exists in between these two. You can imagine other selection criteria, and you'd get different integrals.
Does any of the Henstock-Kurzweil & McShance have any use or role in probability?
Nope. Of course you could try and study other integrals in prob, but you'd need to know the theory well enough and show these integrals have properties which are important in prob and yet don't exist in Lebesgue.
For a prob theory perspective you'll want:
- measure spaces and Polish spaces
- Lebesgue integral
- Ito integral (definitely for stochastic stuff)
Things like H-K integrals are obscure in the literature. You'll know them if you do real analysis, but otherwise never hear of them. I'd be amazed if 3 other people on this forum know how to abstract the H-K integrals
pwsnafu said:woundedtiger4 said:WOW, how many integrals are out in the world?There's an infinite number. The Riemann integral, McShane integral and Henstock-Kurzweil integral are all the same in the sense they are all Riemann sums. The trick is changing which partitions you allow. If you allow lots, you need to restrict f to guarantee the limit existing (Riemann). If you restrict the partitions you can weaken f (H-K). McShane (and hence Lebesgue) exists in between these two. You can imagine other selection criteria, and you'd get different integrals.
Nope. Of course you could try and study other integrals in prob, but you'd need to know the theory well enough and show these integrals have properties which are important in prob and yet don't exist in Lebesgue.
For a prob theory perspective you'll want:
- measure spaces and Polish spaces
- Lebesgue integral
- Ito integral (definitely for stochastic stuff)
Things like H-K integrals are obscure in the literature. You'll know them if you do real analysis, but otherwise never hear of them. I'd be amazed if 3 other people on this forum know how to abstract the H-K integrals
excellent answer... thank you Sir
The Lebesgue integral is a mathematical concept used to calculate the area under a curve in a more general and flexible way than the traditional Riemann integral. It was developed by French mathematician Henri Lebesgue in the early 20th century and is widely used in many areas of mathematics, particularly in analysis and measure theory.
The Lebesgue integral differs from the Riemann integral in several ways. Firstly, it allows for a wider class of functions to be integrated, including those that are not necessarily continuous or have discontinuities. Additionally, the Lebesgue integral takes into account the size of the intervals over which the function is defined, rather than just the values of the function at specific points. This makes it more flexible and powerful in calculating integrals.
The Lebesgue integral can be applied to a wide range of functions, including piecewise continuous functions, step functions, and even functions that are not defined at some points. It can also handle unbounded functions and functions that oscillate rapidly, making it a more versatile tool for integration than the Riemann integral.
To calculate the Lebesgue integral, the function is divided into smaller intervals and the size of each interval is measured. Then, the values of the function over these intervals are multiplied by their respective sizes, and these products are added together to find the total area under the curve. This process is known as the "partition method" and it is the foundation of the Lebesgue integral.
The Lebesgue integral has many practical applications in fields such as physics, engineering, and economics. For example, it can be used to calculate the work done by a varying force, the total charge of a changing electric field, and the expected value of a random variable. It is also used in the study of probability and statistics, where it is used to calculate the probabilities of events based on their likelihoods.