Lebesgue Integration of Simple Functions .... Lindstrom, Lemma 7.4.6 .... ....

[Math Amateur]

I am reading Tom L. Lindstrom's book: Spaces: An Introduction to Real Analysis ... and I am focused on Chapter 7: Measure and Integration ...

I need help with the proof of Lemma 7.4.6 ...

Lemma 7.4.6 and its proof read as follows:

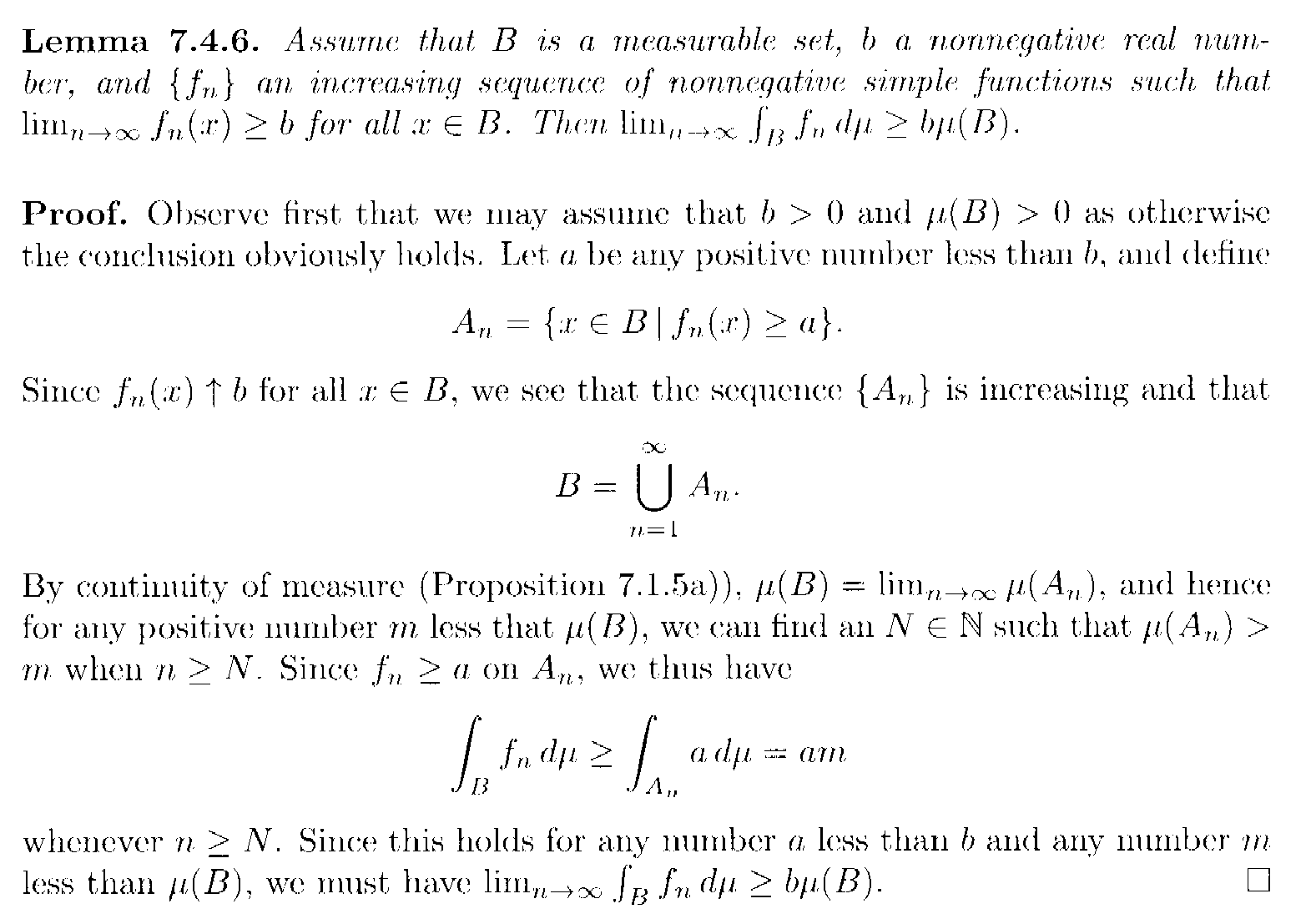
In the above proof by Lindstrom we read the following:

" ... ... Since this holds for any number $$a$$ less than $$b$$ and any number $$m$$ less than $$\mu (B)$$, we must have $$\lim_{ n \to \infty } \int_B f_n d \mu \geq b \mu (B)$$ . ... ... "I need help in order to show, formally and rigorously, that $$\lim_{ n \to \infty } \int_B f_n d \mu \geq b \mu (B)$$ ... ...My thoughts are that we could assume that $$\lim_{ n \to \infty } \int_B f_n d \mu \lt b \mu (B)$$ ... ... and proceed to demonstrate a contradiction ... but I'm not sure how to formally proceed ... ...

Help will be much appreciated ...

Peter

=================================================================================================================


Readers of the above post may be assisted by access to Lindstrom's introduction to the integration of simple functions ... so I am providing access to the relevant text ... as follows:

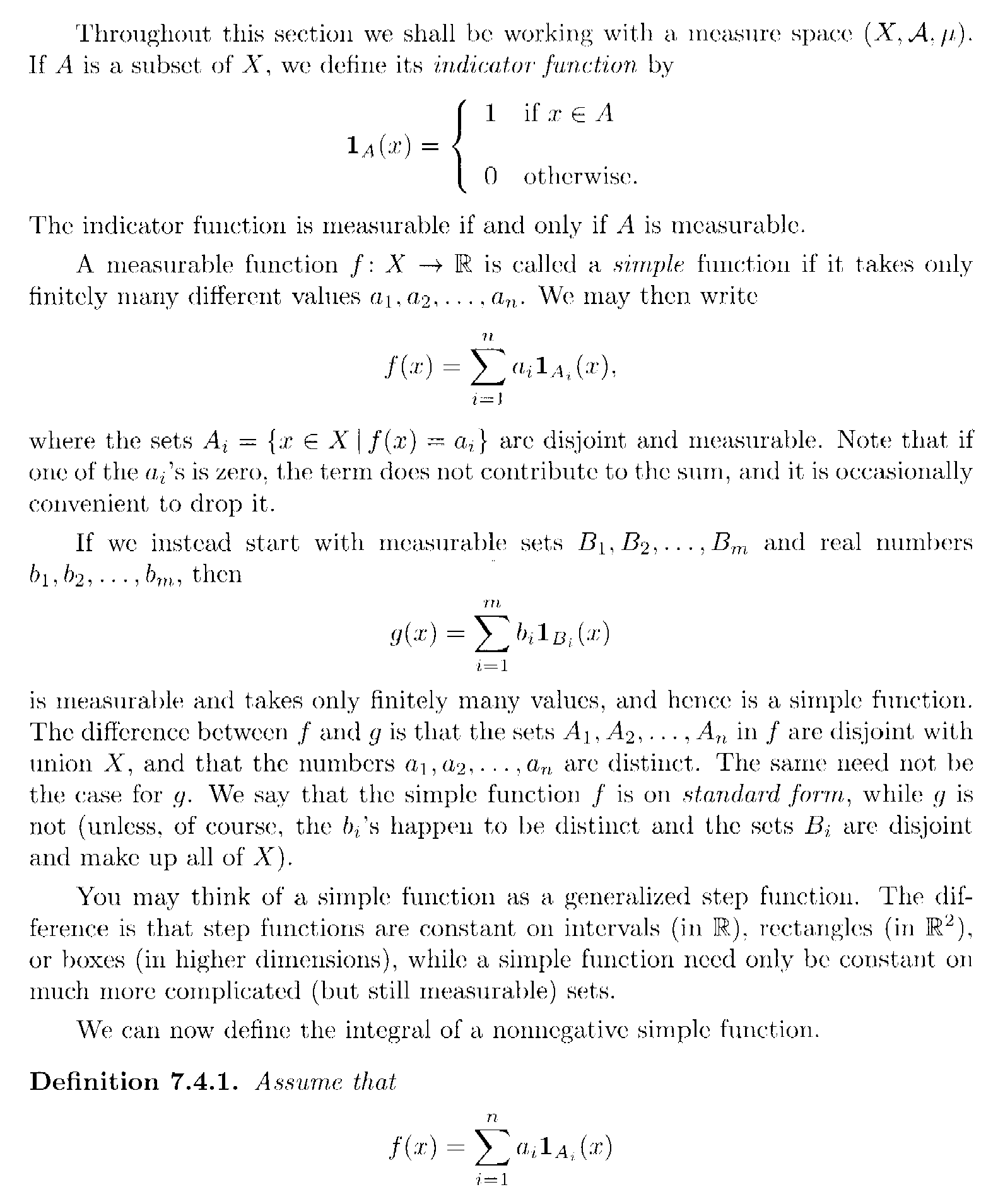
Hope that helps ...

Peter

 

[Opalg]

In the above proof by Lindstrom we read the following:

" ... ... Since this holds for any number $$a$$ less than $$b$$ and any number $$m$$ less than $$\mu (B)$$, we must have $$\lim_{ n \to \infty } \int_B f_n d \mu \geq b \mu (B)$$ . ... ... "I need help in order to show, formally and rigorously, that $$\lim_{ n \to \infty } \int_B f_n d \mu \geq b \mu (B)$$ ... ...

You want formal and rigorous, here it is!

First, Lindstrom appears to assume that $\lim_{n\to\infty}\int_Bf_n\,d\mu$ exists. Since $\left\{\int_Bf_n\,d\mu\right\}$ is an increasing sequence, it will either converge to a finite limit or tend to infinity. I don't know whether Lindstrom allows infinity as a possible limit. Even if he does, we do not need to worry about that case, because if $\int_Bf_n\,d\mu$ does go to infinity it will certainly eventually be larger than $b\mu(B)$.

To prove the inequality, given $\varepsilon>0$, choose $\delta$ such that $0<\delta<\dfrac{\varepsilon}{b+\mu(B)}$. Now choose $a<b$ and $m<\mu(B)$ with $a>b-\delta$ and $m>\mu(B)-\delta$. Then $$b\mu(B) - am = b(\mu(B) - m) + m(b-a) < \delta(b + m) < \delta(b + \mu(B)) = \varepsilon.$$ So $am > b\mu(B) - \varepsilon$. With $N$ as in Lindstrom's proof it follows that$$ \int_Bf_n\,d\mu \geqslant am > b\mu(B) - \varepsilon$$ whenever $n\geqslant N$. Since that holds for all $\varepsilon>0$, $$ \int_Bf_n\,d\mu \geqslant b\mu(B)$$.

[You will recognise that the above argument is just a variant of the proof that the limit of a product is the product of the two limits.]

 

[Math Amateur]

Thanks for a most helpful post Opalg ...

Working carefully through your proof now ...

BUT ... I have another question ...

In the above proof by Lindstrom we read the following:

" ... ... Since $$f_n (x) \uparrow b$$ for all $$x \in B$$ ... ... "Unless I am misunderstanding the notation, $$f_n (x) \uparrow b$$ means $$f_n$$ tends to $$b$$ from below ... but ... all we are given is that $$\lim_{n \to \infty } f_n (x) \geq b$$ which surely is not the same ...

Can someone please clarify this issue ...

Peter

 

[Opalg]

In the above proof by Lindstrom we read the following:

" ... ... Since $$f_n (x) \uparrow b$$ for all $$x \in B$$ ... ... "Unless I am misunderstanding the notation, $$f_n (x) \uparrow b$$ means $$f_n$$ tends to $$b$$ from below ... but ... all we are given is that $$\lim_{n \to \infty } f_n (x) \geq b$$ which surely is not the same ...

I completely agree with you. The statement of the lemma says that $\{f_n\}$ is an increasing sequence and that $\{f_n(x)\}$ has a limit that is greater than or equal to $b$. The statement in the proof of the lemma, that $f_n(x)\uparrow b$, is careless and wrong (because the limit could be greater than $b$). However, the information given in the statement of the lemma is sufficient to ensure that the sequence $\{A_n\}$ is increasing and that $$B = \bigcup_{n=1}^\infty A_n$$, which is what is needed for the rest of the proof to work.

 

[Math Amateur]

Oh ... thanks Opalg ...

Appreciate your help ...

Peter