Lebesgue Outer Measure .... Carothers, Proposition 16.2 (i) ....

[Math Amateur]

I am reading N. L. Carothers' book: "Real Analysis". ... ...

I am focused on Chapter 16: Lebesgue Measure ... ...

I need help with the proof of Proposition 16.2 part (i) ...

Proposition 16.2 and its proof read as follows:

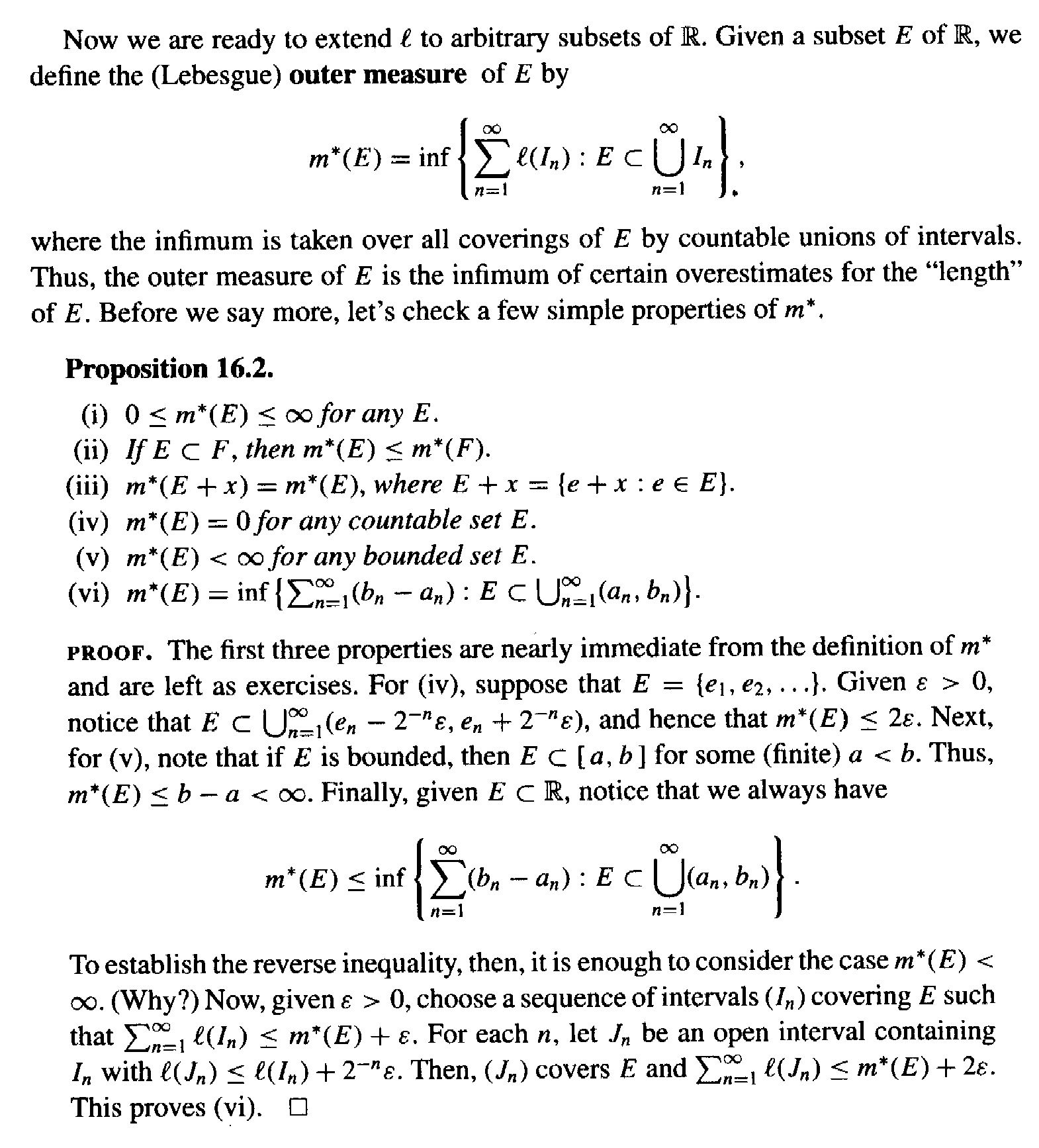
Carothers does not prove Proposition 16.2 (i) above ...

Although it seems intuitively obvious, I am unable to construct and express a valid, convincing, formal and rigorous proof of the result ...

Can someone please demonstrate a formal and rigorous proof of Proposition 16.2 (i) above ...

Peter
========================================================================================================It may help readers of the above post to have access to Carothers introduction to Lebesgue outer measure ... so I am providing the same as follows:

Hope that helps ...

Peter

 

[jvicens]

Dear Peter,

Thank you for reaching out for help with Proposition 16.2 (i) in Carothers' book. I am happy to assist you in constructing a formal and rigorous proof for this proposition.

First, let's review the definition of Lebesgue outer measure, which is denoted by m*(E) for a set E. The Lebesgue outer measure of a set E is defined as the infimum of the sum of the lengths of intervals that cover E. In other words:

m*(E) = inf{∑(b-a) | E ⊆ ∪(a,b)}

where a and b are real numbers representing the endpoints of intervals that cover E.

Now, let's move on to the proof of Proposition 16.2 (i):

Proposition 16.2 (i): For any set E, m*(E) ≥ 0.

Proof:

Assume for contradiction that m*(E) < 0. Then, by definition, there exists a sequence of intervals {I_n} such that E ⊆ ∪(a_n, b_n) and ∑(b_n - a_n) < 0. This implies that ∑(b_n - a_n) is a negative number, which is a contradiction since the sum of lengths of intervals should always be non-negative.

Hence, our assumption that m*(E) < 0 must be false, and therefore m*(E) ≥ 0.

I hope this proof helps you to understand and construct your own formal and rigorous proof for Proposition 16.2 (i). If you have any further questions, please do not hesitate to ask.