Legendre Transformation of Lagrangian density ?

[DOTDO]

Hi

I began to study the basics of QED.

Now I am studying Lagrangian and Hamiltonian densities of Dirac Equation.

I'll call them L density and H density for convenience :)Anyway, the derivation of the H density from L density using Legendre transformation confuses me :(

I thought because parameters of them are space-time components, it should be

But I found that this is related to the De Doner - Weyl Theory,

and the H density used in textbook is

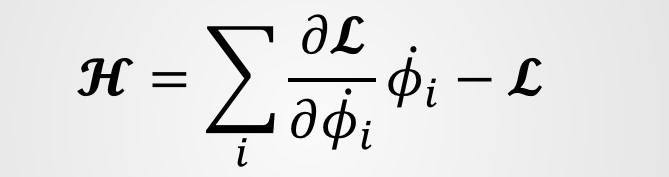
where the dot represents time derivative.So, my question is,

why we consider Legendre transformation on only time derivative of phi ?

Is it just 'defined' to consider energy of the system?

Then what does the covariant H density defined in the De Donder - Weyl theory mean?

 

[robphy]

I hadn't heard of this... but it's interesting.

Possibly enlightening
http://en.wikipedia.org/wiki/De_Donder–Weyl_theory
http://ncatlab.org/nlab/show/de+Donder-Weyl-Hamilton+equation
(also see some of the references)

 

[stevendaryl]

From the lagrangian density \mathcal{L}, you can define the canonical stress-energy tensor \mathcal{T} as follows:

\mathcal{T}^{\mu \nu} = \dfrac{\partial \mathcal{L}}{\partial \partial_\mu \phi_j} \partial^\nu \phi_j - g^{\mu \nu} \mathcal{L}

This is a conserved current in the first index:

\partial_\mu \mathcal{T}^{\mu \nu} = 0

Then you can define a hamiltonian density \mathcal{H} in terms of \mathcal{T}:

\mathcal{H} = \mathcal{T}^{tt} =\dfrac{\partial \mathcal{L}}{\partial \partial_t \phi_j} \partial^t \phi_j - g^{tt} \mathcal{L}

This is the same as the expression in the textbook, if you're using the metric where g^{tt} = +1 and defining \dot{\phi_j} = \partial_t \phi_j

The hamiltonian is the integral of the hamiltonian density over all space:

H = \int d^3 x \mathcal{H}

It's the hamiltonian, not the hamiltonian density, that is constant:

\dfrac{d}{dt} H = 0