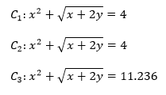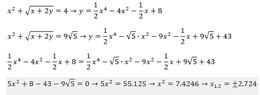Level curves: true / false question

[Yankel]

Hello again,

I have another level curves related question, which I tried solving, but I have the feeling that I did something wrong, would appreciate it if you could have a look.

The question is:

The function f is given by:

\[f(x,y)=x^{2}+\sqrt{x+2y}\]C1 is the level curve that goes through (1,4). C2 is the level curve that goes through (2,-1) and C3 is the level curve that goes through (-3,4).

For each statement, decide true or false:

a. C1=C3
b. C1=C2
c. C1 and C3 do not intersect
d. C2=C3
e. C1 and C2 has exactly two points of intersection

The attached photos show my attempt.

My conclusion is:

a. false
b. true
c. false
d. false
e. false (they are the same, so having more than 2?)

thank you !

 

[Evgeny.Makarov]

I agree with all answers except (c). How can two different level curves intersect?

Concerning the attachment, what is $9\sqrt{5}$ on line 2? Why do the equations of the curves matter at all except to find out if they contain more than two points to answer (e)?

 

[Yankel]

Thank you.

So if I understand you correctly, you are saying that my C1, C2 and C3 are correct, and that c is "true" since two level curves never intersect (yeah, never thought of that). Saying that, when I compared them, shouldn't I have reached a dead end when trying to find shared points ? Is my technique faulty ?

Regarding e, is it correct to say that C1 and C2 represent the same level curve and thus they have infinite number of shared points ?

 

[Evgeny.Makarov]

Saying that, when I compared them, shouldn't I have reached a dead end when trying to find shared points ? Is my technique faulty ?

First, there are errors in the fourth line in the attachment: $\sqrt{5}x^2$ is lost, and $5x^2=55.125$ does not imply $x^2=7.4246$. More importantly, you squared both sides of
\[
x^2+\sqrt{x+2y}=4\tag{*}
\]
and the resulting equation is not equivalent to (*); it may have more solutions. So $x_{1,2}$ you found must be spurious solutions to the problem of intersection of the two curves.

Regarding e, is it correct to say that C1 and C2 represent the same level curve and thus they have infinite number of shared points ?

Yes.