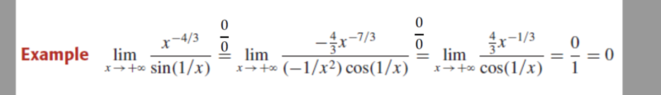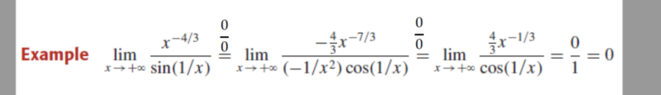- #1
Mohmmad Maaitah
- 87
- 19
- Homework Statement
- How is this 0/0 so we can use L'Hopital's Rule?
- Relevant Equations
- L'Hopital's Rule
I'm talking about the x^(-4/3) how does it equal 0 when x approch infinite??
so I can use
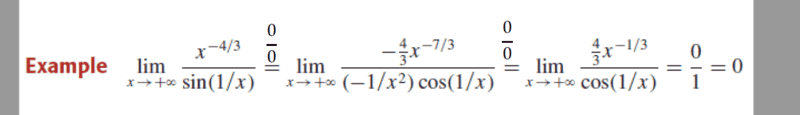
so I can use
According to L'Hopital's Rule, when the limit of a function approaches infinity, the limit of the quotient of the function's derivative and the derivative of the denominator can be used to find the limit. In the case of x^(-4/3), the derivative of the function is (-4/3)x^(-7/3), and the derivative of the denominator is 0. Therefore, the limit can be found by taking the limit of (-4/3)x^(-7/3) as x approaches infinity.
As x approaches infinity, the value of x^(-4/3) becomes increasingly small. This is because as the exponent -4/3 is a negative number, the value of x^(-4/3) will decrease as x increases. As x approaches infinity, the value of x^(-4/3) approaches 0.
No, L'Hopital's Rule can only be used when the limit of a function approaches infinity or negative infinity. It cannot be used for limits approaching any other value.
Yes, L'Hopital's Rule can also be applied when the limit of a function approaches 0/0 or ∞/∞. In these cases, the limit of the quotient of the function's derivative and the derivative of the denominator can be used to find the limit.
No, there are other methods for finding limits approaching infinity, such as using the Squeeze Theorem or graphing the function. However, L'Hopital's Rule is a useful tool for evaluating these types of limits, especially when the function is complex or difficult to graph.
