L’Hôpital’s Rule for indeterminate powers

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

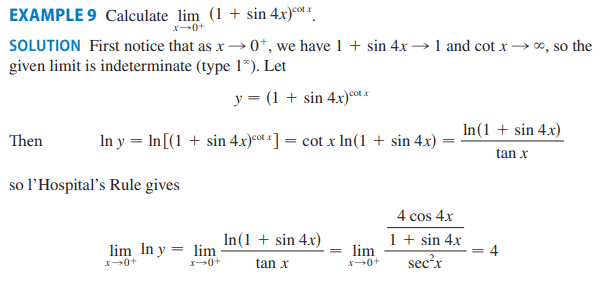
Does someone please know why we are allowed to swap the limit as x approaches zero from the right of y with that of In y?

Thank you for any help!

 

[BvU]

Hi,
Isnt it so that if the limit of the logarithm is 4, then the limit the exercise asks for is $e^4$ ?
I don't see any swapping

x	1+sin(4x)	( )^cot x		e^4
0.1​	1.389418​	26.51954​		54.59815​
0.01​	1.039989​	50.44658​
0.001​	1.004​	54.16361​
0.0001​	1.0004​	54.55449​
0.00001​	1.00004​	54.59378​

$\$

 

[FactChecker]

Continuity of the function ln() at 1. Of course, the answer will have to be converted back, so 4 is not the final answer.

 

[pasmith]

I think it's continuity of exp we need, since we're not pulling the limit inside the log. $$\lim_{x \to a} f(x) = \lim_{x \to a} \exp(\ln f(x)) = \exp(\lim_{x \to a} \ln f(x)).$$

 

[FactChecker]

I think it's continuity of exp we need, since we're not pulling the limit inside the log. $$\lim_{x \to a} f(x) = \lim_{x \to a} \exp(\ln f(x)) = \exp(\lim_{x \to a} \ln f(x)).$$

Good point. But I think we need the continuity of the log at one point and the continuity of exp at the end to undo what was done with the log.

 

[pasmith]

Clearly it doesn't help us to look at $g\left(\lim_{x \to a} g^{-1}(f(x))\right)$ if we can't say anything about the behaviour of $g^{-1}\circ f$ near $a$.

 

[FactChecker]

Clearly it doesn't help us to look at $g\left(\lim_{x \to a} g^{-1}(f(x))\right)$ if we can't say anything about the behaviour of $g^{-1}\circ f$ near $a$.

I see your point. Although the continuity of ln() is good motivation for taking logs, it is not an essential part of the proof.

 

[Mark44]

Isnt it so that if the limit of the logarithm is 4, then the limit the exercise asks for is e⁴?
I don't see any swapping

The swapping occurs in going from $\lim_{x \to 0^+} \ln y = \dots = 4$ to the next equation which isn't shown. Namely, $\lim_{x \to 0^+} \ln y = \ln(\lim_{x \to 0^+} <\text{stuff}>) = 4$. Here the limit operation and natural log are swapped.
From this we conclude that the original expression has a limit of $e^4$.

Although the continuity of ln() is good motivation for taking logs, it is not an essential part of the proof.

Taking logs of both sides is the standard way of dealing with the limits of exponential expressions where the variable occurs in the exponent and possibly elsewhere.