Lifting an object through water (force needed)

[gloo]

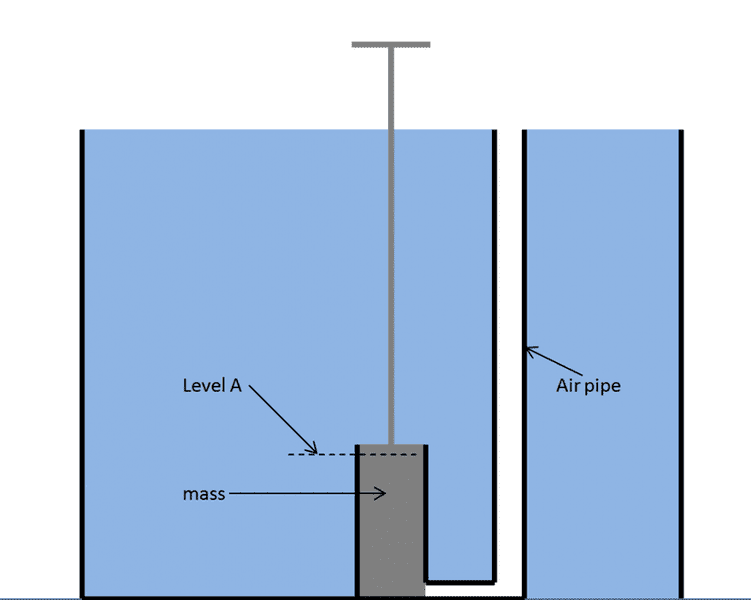
My question is, for the diagram attached. The set up is:

1. The object (gray), including the handle , weighs 2000 Newtons
2. The object is not open to the water below it but there is an air pipe that allows for air above to fill in the pipe
3. The object is snug against the wall (in black), so as to not allow water to seep between and into the pipe area

If a constant upward force of 2000 Newtons is used to pull the entire object up so the bottom of the object is at Level A, is the force large enough? I assume that the water above it is not lifted but gets moved to the side as it "falls" over the top of the object. (Assume there is zero friction).

I know the speed will be reduced, but will the constantly applied force large enough to eventually lift the bottom of the object to Level A?

 

[Doc Al]

I assume that the water above it is not lifted but gets moved to the side as it "falls" over the top of the object.

The water above still exerts a downward force on the object that must be overcome.

 

[russ_watters]

The answer depends on the depth of the water and geometry of the object, since the water is pushing down on it.

 

[andrewkirk]

Giving the object's weight rather than its mass creates an ambiguity, because we need to know whether 2000N is the weight in vacuum, air or in water, although the difference between the first two is small enough to be ignored for practical purposes. The difference between weights in air and water is the buoyancy.
Let's assume 2000N is the weight in a vacuum.
Then the net force on the object is 2000N down plus the sum of all the pressure forces on it from the water against all its surfaces, plus the force of the pipe mouth against the object (which will push left, as the object is pushed right against the pipe by pressure).
You need to include the base of the object in the surfaces subject to the pressure force because even though there will be only a few molecules of water between the tank floor and the object base, they will exert the same pressure as when the object is clear of the floor. To see that consider the difference between trying to lift a CD off a table and trying to lift a silicon sucker of the same shape and size off the table. If the base of the object and the floor of the tank were smooth enough to create a 'sucker' effect, the answer would be very different. But for ordinary everyday objects they won't be.

If the object has height h and horizontal cross sectional area A, what result do you get for the upward force from the water (the buoyancy) when you add up the pressure forces on all the object's surfaces? For simplicity, assume all surfaces are either purely horizontal or purely vertical.

Although the size of the object will determine the size of the buoyancy, it doesn't affect whether the buoyancy is more than zero, which is all you need to know to answer the question.

 

[gloo]

The answer depends on the depth of the water and geometry of the object, since the water is pushing down on it.

I guess, the geometry is as shown -- flat top. And for the depth let's assume 20 meters between the surface of the water and the top of the object where the water rests?
If the object is say 5 meters by 5 meters on top...then there is 500 cubic meters of water for a force of 4,905,000 Newtons (approx). The pressure on top 196 Kpa.
If the lifting distance is say 8 meters I know I am not lifting 200 cubic meters of water (5m x 5m * 8m). How do I account for the needed force to move the water out of the way to the sides?

 

[gloo]

Giving the object's weight rather than its mass creates an ambiguity, because we need to know whether 2000N is the weight in vacuum, air or in water, although the difference between the first two is small enough to be ignored for practical purposes. The difference between weights in air and water is the buoyancy.
Let's assume 2000N is the weight in a vacuum.
Then the net force on the object is 2000N down plus the sum of all the pressure forces on it from the water against all its surfaces, plus the force of the pipe mouth against the object (which will push left, as the object is pushed right against the pipe by pressure).
You need to include the base of the object in the surfaces subject to the pressure force because even though there will be only a few molecules of water between the tank floor and the object base, they will exert the same pressure as when the object is clear of the floor. To see that consider the difference between trying to lift a CD off a table and trying to lift a silicon sucker of the same shape and size off the table. If the base of the object and the floor of the tank were smooth enough to create a 'sucker' effect, the answer would be very different. But for ordinary everyday objects they won't be.

If the object has height h and horizontal cross sectional area A, what result do you get for the upward force from the water (the buoyancy) when you add up the pressure forces on all the object's surfaces? For simplicity, assume all surfaces are either purely horizontal or purely vertical.

Although the size of the object will determine the size of the buoyancy, it doesn't affect whether the buoyancy is more than zero, which is all you need to know to answer the question.

Will I assumed away the friction to simplify; also the bottom of the object...let's just say there was small pillar supports the raise it off the bottom of the floor (no sucker effect). I assume there is no buoyancy because water does not fill up in the pipe and add any upward water pressure.

 

[russ_watters]

Force is pressure times area. This problem is as simple as that.

I know I am not lifting 200 cubic meters of water (5m x 5m * 8m).

Why not? Where else is it going to go?

 

[Doc Al]

I assume there is no buoyancy because water does not fill up in the pipe and add any upward water pressure.

But there's water pushing down on the top of the object. As Russ said, to find the downward force from the water, use pressure times area.

 

[andrewkirk]

It seems to me that the purpose of the exercise is to embed an understanding that pressure within a fluid operates in all directions, and to appreciate the consequences of that.
The diagram makes it all rather trivial because, as soon as the object is raised one mm, water will rush into the pipe beneath it, the level of water in the pipe will equalize with the rest of the tank, and the pipe will become irrelevant.
It would have been better to have drawn it with the top of the lower outlet of the pipe level with the top of the object, so that the object blocks water from entering the pipe for nearly all of the time it is being lifted.
If the diagram had instead been drawn that way, what would be the impact of the air-filled pipe during the period between the commencement of lifting and when water starts to enter the pipe (which will now only happen when the lifting is nearly finished)?

 

[Doc Al]

The diagram makes it all rather trivial because, as soon as the object is raised one mm, water will rush into the pipe beneath it,

The object-pipe seal is water tight. When the object raises a bit, air will rush in, not water. (At least that's how I understand the problem.)

 

[jbriggs444]

The object-pipe seal is water tight. When the object raises a bit, air will rush in, not water. (At least that's how I understand the problem.)

I think the point being made is that the inlet depicted on the pipe to the right is exactly at water level and is not [shown as being] water tight. Raise the water level a bit and water will begin to trickle in.

 

[Doc Al]

I think the point being made is that the inlet depicted on the pipe to the right is exactly at water level and is not [shown as being] water tight. Raise the water level a bit and water will begin to trickle in.

Ah, good point. (I had just assumed that the pipe extended further, despite the drawing, as no mention was made of that issue.)

 

[Doc Al]

@gloo Did you mean for the top of the air pipe to be at the exact height of the initial water level (as you drew it) so that water begins trickling in as the object is raised?

 

[gloo]

@gloo Did you mean for the top of the air pipe to be at the exact height of the initial water level (as you drew it) so that water begins trickling in as the object is raised?

No, I did mean that no water would trickle in-- the air pipe would allow air to fill the spot where the object was raised. If water filled in I do understand that buoyant water pressure equal to the height of the surface to the bottom of the object would result in an additional force of buoyancy...but I wanted to obviate that. I just thought, since I am not lifting any molecules upward...they get pushed to the side and "fall over" the edge of the object, water is not being raised upward against the gravity, but pushed sideways --- thought that meant different type of calculation. I understand that if you would raise the object by 8 meters, and say there was walls that led all the way to the surface, you would raise all the molecules of water directly above which would require a huge force ( about 5 million Newtons). I just couldn't resolve that problem in my head.

 

[Doc Al]

No, I did mean that no water would trickle in-- the air pipe would allow air to fill the spot where the object was raised.

You might want to extend the pipe up above the initial water level, as the water level will rise as the object is lifted and displaces water.

I just thought, since I am not lifting any molecules upward...they get pushed to the side and "fall over" the edge of the object, water is not being raised upward against the gravity, but pushed sideways

The lifting object displaces water and thus the water level will rise. If the air pipe opening is exactly at the initial water level, then water will start trickling in (as others have pointed out).

 

[russ_watters]

I just thought, since I am not lifting any molecules upward...they get pushed to the side and "fall over" the edge of the object, water is not being raised upward against the gravity...

Again, that isn't true: there is other water in the way to the sides, so the water can go nowhere else but up. You essentially are raising a column of water and spilling it out onto the top surface of the tank water as you lift the object.

 

[andrewkirk]

No, I did mean that no water would trickle in-- the air pipe would allow air to fill the spot where the object was raised.

Ah. that puts a different complexion on the problem. As I understand it now, the grey object - say it's a rectangular prism, is encased in a tight fitting casing (a 'sleeve') that is fixed to the bottom of the tank and connected to the air pipe. If subjected to enough force, the grey object can move in that sleeve like a piston. Previously, it was not clear to me that the object was encased in a watertight sleeve.

With that setup, water pressure acts on the top of the grey object, not on the bottom. So there is the same effect as with a sucker. Hence the force required to lift the object is its vacuum weight (earlier assumed to be 2000N) plus the weight of the water column above it, which will be proportional to the object's cross sectional area and the height of that column (depth of the object). But whatever it is, it will be more than zero, so more than 2000N will be needed to move the object.
There will be a very slight buoyancy provided by air coming in underneath the object. But that is trivial compared to the weight of water, and can be ignored.

 

[Doc Al]

There will be a very slight buoyancy provided by air coming in underneath the object. But that is trivial compared to the weight of water, and can be ignored.

Once the air flows under the object, the resulting upward air pressure will cancel out the air pressure presumably pushing down on the water surface.