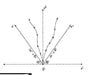
- #1
JonnyMaddox
- 74
- 1
Hi guys, I'm trying to understand light cone coordinates for which I uploaded this picture. The light cone coordinates are given by
[itex]x^{+}= \frac{1}{\sqrt{2}} (x^{0}+x^{1})[/itex]
[itex]x^{-}= \frac{1}{\sqrt{2}} (x^{0}-x^{1})[/itex]
Now how should I think of this? I guess the space curves do only life in the space that is spanned by the [itex]x^{0}[/itex] and [itex]x^{1}[/latex] axes. But what does it mean that a light curve is zero in this coordinate system?
[itex]x^{+}= \frac{1}{\sqrt{2}} (x^{0}+x^{1})[/itex]
[itex]x^{-}= \frac{1}{\sqrt{2}} (x^{0}-x^{1})[/itex]
Now how should I think of this? I guess the space curves do only life in the space that is spanned by the [itex]x^{0}[/itex] and [itex]x^{1}[/latex] axes. But what does it mean that a light curve is zero in this coordinate system?