Limit calculation involving log and trig functions

[kshitij]

Homework Statement

(see attached)

Relevant Equations

-

This was the question,

The above solution is the one that I got originally by the question setters,
Below are my attempts (I don't know why is the size of image automatically reduced but hope that its clear enough to understand),

As you can see that both these methods give different answers and both of which are wrong.

I checked my attempts using wolfram and found that upto this point in method I,

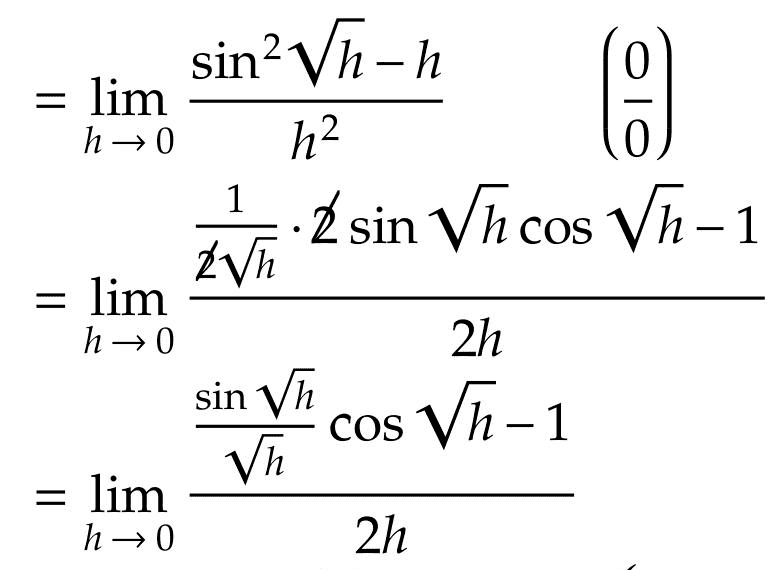
This limit matches the correct answer according to wolfram,

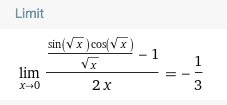
And similarly in method II upto this step,

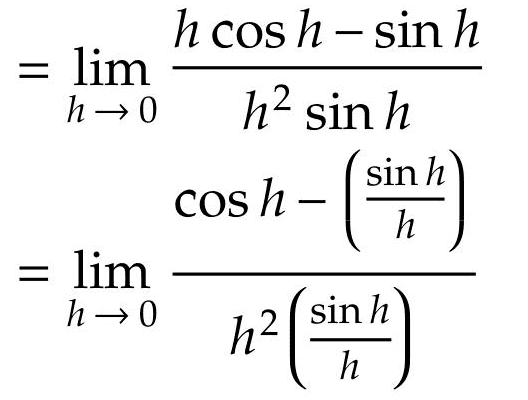
The limit matches the answer,

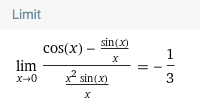
So, I think that when I substituted (for some reasons LaTeX is not working)

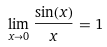, It all got wrong but why? Why can't we substitute that? Even in the original solution they substituted

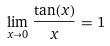and yet their answer is correct so why is my attempt wrong?

(P.S. sorry for all those attachments, I had already typed all these earlier and didn't want to redo this in LaTeX and if those images of my attempt aren't clear to read you can see the full image here)

 

[Delta2]

You just can't apply the quotient rule of the limit (that $$\lim_{h\to h_0} \frac{f(h)}{g(h)}=\frac{\lim_{h \to h_0} f(h)}{\lim_{h\to h_0} g(h)}$$)in this way because it leads to 0/0. The quotient rule of limit can be applied only if the denominator (that is $\lim_{h\to h_0} g(h)$) is not zero.

 

[kshitij]

You just can't apply the quotient rule of the limit (that $$\lim_{h\to h_0} \frac{f(h)}{g(h)}=\frac{\lim_{h \to h_0} f(h)}{\lim_{h\to h_0} g(h)}$$)in this way because it leads to 0/0. The quotient rule of limit can be applied only if the denominator (that is $\lim_{h\to h_0} g(h)$) is not zero.

I didn't knew that!

But in the original solution also they used the quotient rule even though both the numerator and denominator is zero. Is that also incorrect?

 

[Delta2]

No they don't actually use it, they see it leads to 0/0 and they use L'Hospital rule instead.

 

[kshitij]

No they don't actually use it, they see it leads to 0/0 and they use L'Hospital rule instead.

I don't think I understand what you're saying, I was talking about the last step
$$\lim_{h\to 0} \frac{h-\tan h}{h^2 \cdot \tan h}=\lim_{h\to 0} \frac{h-\tan h}{h^3 \cdot \frac{\tan h}{h}}=\frac{\lim_{h \to 0} h-\tan h}{\lim_{h\to 0} h^3 \cdot \frac{\tan h}{h}}=\frac{\lim_{h \to 0} h-\tan h}{\lim_{h\to 0} h^3 }=\lim_{h\to 0} \frac{h-\tan h}{h^3}$$

 

[Delta2]

No the last step doesn't go like this. They don't use the quotient rule except in the very last step (which is not shown) after they have done some algebra which removes the 0/0 form. It goes as follows.

$$=\lim_{h \to 0} \frac{-1}{3\frac{\tan\theta}{\theta}}+\frac{...}{\theta ^3\frac{tan\theta}{\theta}}$$ where the $...$ contains a sum of powers of $\theta$ which are greater than 3 so that term is actually a sum of terms of $\frac{\theta^k}{\frac{\tan\theta}{\theta}}$ for $k>0$ which of course is not of the type 0/0 but 0/1=0.

 

[kshitij]

No the last step doesn't go like this. They don't use the quotient rule except in the very last step (which is not shown) after they have done some algebra which removes the 0/0 form. It goes as follows.

$$=\lim_{h \to 0} \frac{-1}{3\frac{\tan\theta}{\theta}}+\frac{...}{\theta ^3\frac{tan\theta}{\theta}}$$ where the $...$ contains a sum of powers of $\theta$ which are greater than 3 so that term is actually a sum of terms of $\frac{\theta^k}{\frac{\tan\theta}{\theta}}$ for $k>0$ which of course is not of the type 0/0 but 0/1=0.

That makes sense, Thank you!