- #1
Waxterzz
- 82
- 0
Hi,
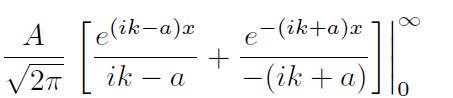
The two terms should vanish at infinity according to the Quantum textbook of Griffiths, but I don't see how?
I mean a complex exponential is a periodic function so how can it vanish at infinity?
If you split up the first term
exp(ikx) * exp(-ax)
Take the limit of infinity of this expression
lim exp(ikx) is not defined
limit exp(-ax) turns zero
But 0 * an undefined limit is still undefined, right?
So help me out, please.
The two terms should vanish at infinity according to the Quantum textbook of Griffiths, but I don't see how?
I mean a complex exponential is a periodic function so how can it vanish at infinity?
If you split up the first term
exp(ikx) * exp(-ax)
Take the limit of infinity of this expression
lim exp(ikx) is not defined
limit exp(-ax) turns zero
But 0 * an undefined limit is still undefined, right?
So help me out, please.
Last edited: