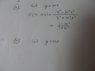Limits of a Function: Q45 - Can't Figure It Out

[athrun200]

Homework Statement

See the first photo.Q45

Can I use the method similar to 43?
I don't understand what does "condering (x,0,0)or (0,y,0) mean.

Homework Equations

The Attempt at a Solution

see photo 2.
I only know how to do 43
I have no idea for 45

 

[vela]

For a limit to exist, you can't get different answers depending on the direction you approach a point. When the problem says to consider points of the form (x,0,0), it's asking you to calculate the limit as you approach the origin along the x-axis.

 

[SammyS]

BTW: What do you conclude about #43?

 

[flyingpig]

For 45 try this

f(x,y,z) = \frac{x + y + z}{x^2 + y^2 + z^2}

What happens when you cut with x = x and with y,z =0? What happens to f?

 

[athrun200]

For 45 try this

f(x,y,z) = \frac{x + y + z}{x^2 + y^2 + z^2}

What happens when you cut with x = x and with y,z =0? What happens to f?

It becomes \frac{1}{x}
Then, as x\rightarrow0, f(x,y,z) doesn't exist?

 

[athrun200]

BTW: What do you conclude about #43?

It seems if we have denominator, then the function is not continuous at origin.

 

[HallsofIvy]

? The problem does not ask about continuity, only about the limit at the point. It is possible for the denominator of a fraction to go to 0 and the limit still exist at that point.

In problem 43,
\lim_{(x,y)\to (0,0)}\frac{x^2- y^2}{x^2+ y^2}
if we take y= mx, as suggested, we get
\frac{x^2- m^2x^2}{x^2+m^2x^2}= \frac{x^2(1- m^2)}{x^2(1+ m^2)}= \frac{1- m^2}{1+ m^2}
as long as x is not 0.

If the limit exists, then the limit of that should be the same for all m. Is it?

 

[athrun200]

It seems we use the similar method to prove continunity. If not, how do I prove that problem 43 continuous at (0,0)?