- #1
Tony Stark
- 51
- 2
The line element is defined as
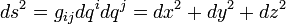
How is dx2+dy2+dz2 be written as gijdqidqj.
Is some sort of notation used??
How is dx2+dy2+dz2 be written as gijdqidqj.
Is some sort of notation used??
