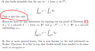- #1
youngurlee
- 19
- 0
I have shown by my intuition that if a good field g(2th or more differentiable) in n dimension satisfies
[itex]\frac{∂g_{i}}{∂x_{j}}-\frac{∂g_{j}}{∂x_{i}}[/itex]=0 for all i,j,
then [itex]\oint[/itex]g[itex]\cdot[/itex]dl=0,
hence there exist a scalar function [itex]\phi[/itex] such that
[itex]\frac{∂\phi}{∂x_{i}}=g_{i}[/itex] for all i.
I want to know what in general will the ring integral [itex]\oint[/itex]g[itex]\cdot[/itex]dl be,
can it be written as a surface integral, as in Kelvin–Stokes theorem?
[itex]\frac{∂g_{i}}{∂x_{j}}-\frac{∂g_{j}}{∂x_{i}}[/itex]=0 for all i,j,
then [itex]\oint[/itex]g[itex]\cdot[/itex]dl=0,
hence there exist a scalar function [itex]\phi[/itex] such that
[itex]\frac{∂\phi}{∂x_{i}}=g_{i}[/itex] for all i.
I want to know what in general will the ring integral [itex]\oint[/itex]g[itex]\cdot[/itex]dl be,
can it be written as a surface integral, as in Kelvin–Stokes theorem?