Line integral of a vector field.

[Jack_O]

Hi all, I'm new to the forums so if i do something stupid don't hesitate to tell me.

Anyway I'm struggling with this problem:

I could do part a ok, but part b has me stumped, I am in the second year of a physics degree and this is a from a maths problem sheet, i haven't done line integrals before now and they have me a bit confused, my textbook has a few examples but none of them include vectors and http://en.wikipedia.org/wiki/Line_integral" has me even more confused.

Here is my attempt so far:

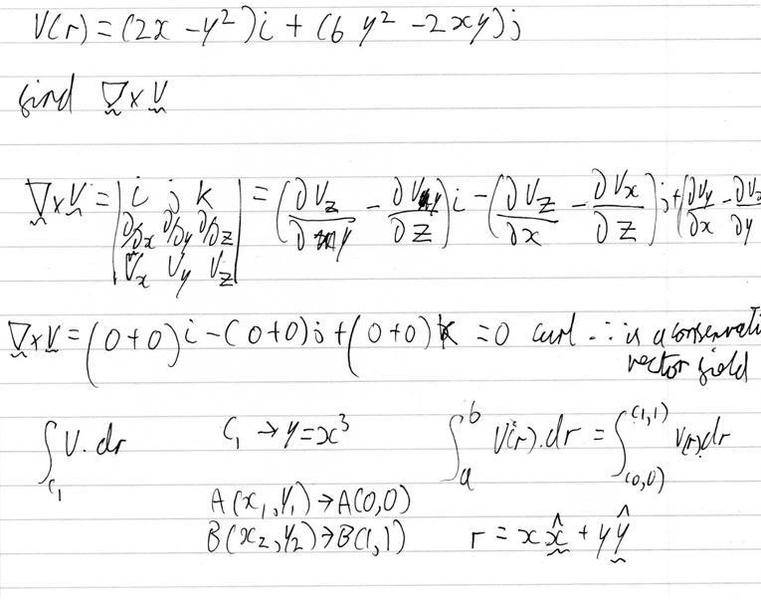
(please excuse bad handwriting, i am dyslexic)

I basically don't know where to begin with it, any help much appreciated.

 

[Dick]

Use that along your path y=x^3. So r=x*i+x^3*j. (i=x hat and j=y hat). What is the vector dr? Change the y's in V to x^3's as well and integrate dx.

 

[Jack_O]

I think dr is just a small difference in the postion vector r, so dr = dx*i+dy*j ? r isn't mentioned anywhere else in the question.

 

[Dick]

I think dr is just a small difference in the postion vector r, so dr = dx*i+dy*j ? r isn't mentioned anywhere else in the question.

Sure it is. But now let's decide to integrate dx. Replace y with x^3. Now what's dr?

 

[Jack_O]

dr=x*i +(x^3)j

I also have V(r)=(2x-x^6)i + [(6x^6)-(2x^4)]j

But i am a bit unsure about V.dr, is it {[ (2x^2)-(x^7) ]i + [ (6x^9)-(2x^7) ]j}dx ?

 

[Dick]

What happened to the 'd's on the right side of dr? You've got y*j, shouldn't it be d(y)*j? Same for i. Let's get dr right before going to the dot product.

 

[Jack_O]

OK, i jumped the gun a bit with dr, is it d(r) = d(x)*i + d(y)*j = d(x)*i + d(x^3)*j ?

 

[Dick]

Right. And d(x^3)=3*x^2*dx, right? So dr=(i+3x^2*j)dx.Now do the dot product and you'll get a single integral dx.

 

[Jack_O]

Ok, V.dr=[(2x-x^6)+(18x^8)-(6x^6)]dx

When i integrate this with the limits x1=0 and x2=1 i get 2, does this sound about right?

 

[Dick]

Ok, V.dr=[(2x-x^6)+(18x^8)-(6x^6)]dx

When i integrate this with the limits x1=0 and x2=1 i get 2, does this sound about right?

That's what I got. Not so hard, hmm?

 

[Jack_O]

That's what I got. Not so hard, hmm?

Yeah thanks that's been a great help.

Part c seems trivial now but part d seems a bit daunting still.

 

[Dick]

Don't be daunted. You know dphi/dx=2x-y^2 (partial derivative). What does that tell you about phi?

 

[Jack_O]

Hmm, after much head scratching i think what you are getting at is that $$\nabla$$(phi(x,y))=(dphi/dx)i+(dphi/dy)j, which means:

phi(x,y)=[int(2x-y^2)dx] + [int((6y^2)-2xy)]

which gives:

phi=x² + 2y³ -xy²

Which does seem to give 2 when i do phi(1,1) - phi(0,0)

 

[Dick]

The answer is right. Since dphi/dx=2x-y^2, that means phi=x^2-x*y^2+f(y). Yeah, that is 'integral dx' with f(y) being the constant of integration. That gives dphi/dy=-2xy+f'(y). Since you are supposed to get 6y^2-2xy, you can figure that the f'(y) part must be the 6y^2, so if you put it all together, phi=x^2-xy^2+2y^3.

 

[Dick]

Hmm, after much head scratching i think what you are getting at is that $$\nabla$$(phi(x,y))=(dphi/dx)i+(dphi/dy)j, which means:

phi(x,y)=[int(2x-y^2)dx] + [int((6y^2)-2xy)]

which gives:

phi=x² + 2y³ -xy²

Which does seem to give 2 when i do phi(1,1) - phi(0,0)

I'm not taking your int()+int() formula literally. If I did I would get a -xy^2 term from each one of those. For a total of -2xy^2, which is not right.

 

[Jack_O]

Well I've managed to do the problem, and i could probably do others now using that technique, but I'm not sure i understand why it works, i mean in questions b, c and d the only constant is x1=0, y1=0, x2=1 and y2=1, why doesn't the chosen path have an effect, is it something to do with the curl being 0?

 

[Dick]

It has everything to do with the curl being zero. It's one of the conditions you need for V to be conservative. 'Conservative' means that the line integral between two points is independent of the path chosen. If they hadn't given you a conservative V, then the answer would depend on the path.

 

[Jack_O]

Ok i get it now! Thanks for your help, i wouldn't have been able to do this much without it.