Line Integral Solution for Curve γ: Simplifying Substitutions

[Graham87]

Homework Statement

Solve this line integral

Relevant Equations

see pictures

Hello,

How should I go about to solve this line integral along the line curve γ?

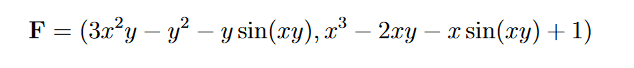
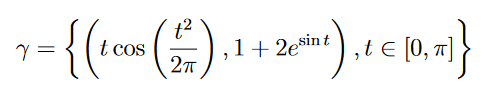I attempt to apply this relation but the substitutions get too messy.

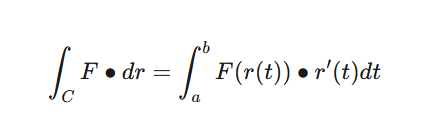
Thanks

 

[Orodruin]

can you make any particular observations regarding the relation between the two components of your vector field?

 

[Graham87]

can you make any particular observations regarding the relation between the two components of your vector field?

I'm not sure. It looks overwhelmingly complicated to me.
Should I try to check if it is path independent?

 

[Steve4Physics]

I'm not sure. It looks overwhelmingly complicated to me.
Should I try to check if it is path independent?

You might want to consider the start and end coordinates of the path (corresponding to $t=0$ and $t= \pi$). You might want to consider whether or not the field is conservative.

Edited.

 

[Orodruin]

I'm not sure. It looks overwhelmingly complicated to me.
Should I try to check if it is path independent?

Compare the first terms of each expression. What do you see?
Do the same for the second and third terms. Same question.
Do the same for the fourth term (which is 0 for the x-component). Same question.

If you prefer to check in a different way if the field is conservative, please feel free to do so.

 

[Graham87]

Compare the first terms of each expression. What do you see?
Do the same for the second and third terms. Same question.
Do the same for the fourth term (which is 0 for the x-component). Same question.

If you prefer to check in a different way if the field is conservative, please feel free to do so.

Looks like some derivative or primitive function variation. But it's not in a series.
I might consider checking if the field is conservative. But I'm curious how it would be done by the other way?

 

[Orodruin]

Looks like some derivative or primitive function variation. But it's not in a series.
I might consider checking if the field is conservative. But I'm curious how it would be done by the other way?

There is really no "magic" too it. Just that $3 x^2 y$ is quite clearly the $x$-derivative of $x^3 y$ ... of which $x^3$ is the $y$-derivative, etc etc