ashah99
- 55
- 2
- Homework Statement
- Please see attached photo for problem statement.
- Relevant Equations
- LU Factorization concepts
Hello all, I have a problem related to LU Factorization with my work following it. Would anyone be willing to provide feedback on if my work is a correct approach/answer and help if it needs more work? Thanks in advance.
Problem:

Work:
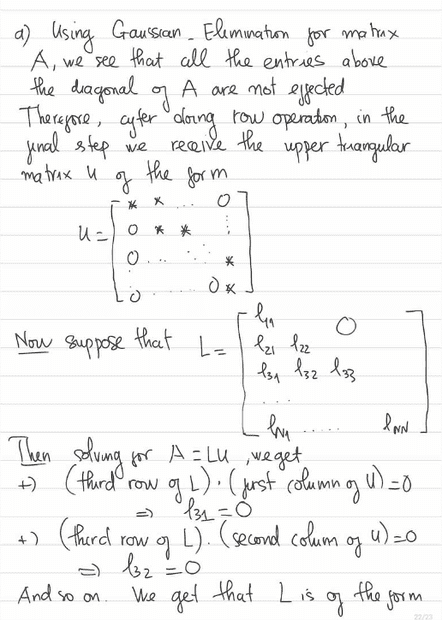

Problem:
Work: