- #1
xidios
- 8
- 0
Misplaced Homework Thread
Summary:: Linear algebra
1.Let a a fixed vector of the Euclidean space E, a is a fixed real number. Is there a set of all vectors from E for which (x, a) = d the linear subspace E /
2.
Let nxn be a matrix A that is not degenerate. Prove that the characteristic polynomials f (λ) of the matrix A and h (λ) of the matrix A ^ -1 are related by
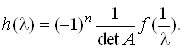
3. Prove that the functions e ^ -t, e ^ -2t, e ^ -3t are linearly independent on [0,infinity)
Please help
1.Let a a fixed vector of the Euclidean space E, a is a fixed real number. Is there a set of all vectors from E for which (x, a) = d the linear subspace E /
2.
Let nxn be a matrix A that is not degenerate. Prove that the characteristic polynomials f (λ) of the matrix A and h (λ) of the matrix A ^ -1 are related by
3. Prove that the functions e ^ -t, e ^ -2t, e ^ -3t are linearly independent on [0,infinity)
Please help
Last edited by a moderator: