jaredjjj
- 5
- 0
Have I solved this linear approximation question correctly?
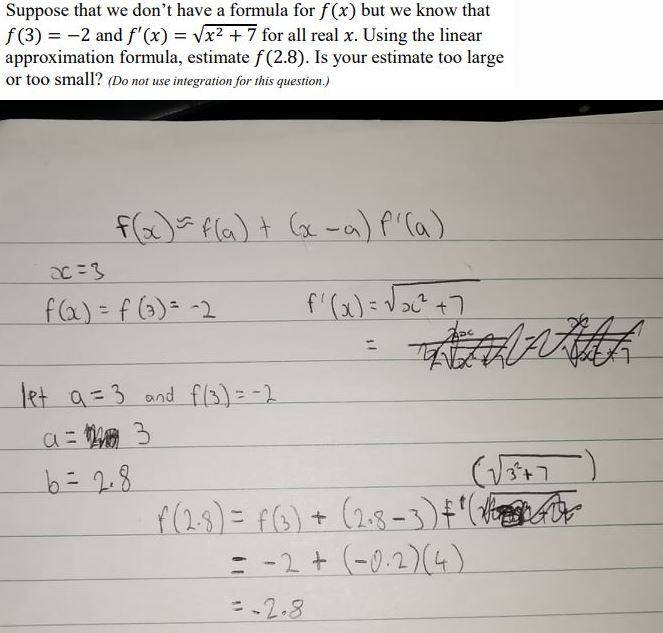
To answer the second half do I have to use the formula f'(x)=sqrt(x^2+7) which would mean -2.8 would be approximately equal to 3.852 which is the same as 2.8.skeeter said:yes, $f(2.8) \approx -2.8$
now, how to determine if that value is an over or under estimate?
jaredjjj said:To answer the second half do I have to use the formula f'(x)=sqrt(x^2+7) which would mean -2.8 would be approximately equal to 3.852 which is the same as 2.8.