- #1
bwpbruce
- 60
- 1
Question:
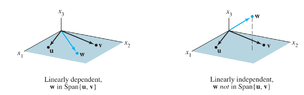
If \(\displaystyle \textbf{v}_1,...,\textbf{v}_4\) are in \(\displaystyle \mathbb{R}^4\) and \(\displaystyle \{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3\}\) is linearly dependent, is \(\displaystyle \{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3, \textbf{v}_4\}\) also linearly dependent?
My Solution:
http://s29.postimg.org/4wvwjlkqd/Linearly_Independent_Sets.png
If \(\displaystyle \textbf{v}_1,...,\textbf{v}_4\) are in \(\displaystyle \mathbb{R}^4\) and \(\displaystyle \{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3\}\) is linearly dependent, is \(\displaystyle \{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3, \textbf{v}_4\}\) also linearly dependent?
My Solution:
http://s29.postimg.org/4wvwjlkqd/Linearly_Independent_Sets.png