Linear Map Problem: Proving Equivalence of a & b

[Fernando Revilla]

I quote an unsolved problem from MHF (Linear map problem) posted by user jdm900712

et V be a vector space over the field F. and T

L(V, V) be a linear map.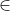

Show that the following are equivalent:
a) I am T

Ker T = {0}
b) If T^2(v) = 0 -> T(v) = 0, v

V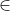
Using p -> (q -> r) <-> (p

q) ->r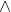
I suppose I am T

Ker T = {0} and T

(v) = 0.
then I know that T(v)

Ker T and T(v)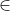

I am T
so T(v) = 0.
I need help on how to prove the other direction.

http://mathhelpforum.com/advanced-algebra/212908-linear-map-problem.html

 

[Fernando Revilla]

We have to prove $\mbox{Im }T\cap \ker T=\{0\}\Leftrightarrow (T^2(v)=0\Rightarrow T(v)=0)$

$\Rightarrow)$ Suppose $T^2(v)=0$, then $T(T(v))=0$. But $T(v)\in \mbox{Im }T$ (by definition of image) and $T(v)\in \ker T$. By hypothesis, $T(v)=0$.

$\Leftarrow)$ Suppose $x\in\mbox{Im }T\cap \ker T$ then, $x\in\mbox{Im }T$ and $x\in \ker T$, that is $x$ has de form $x=T(w)$ and $T(x)=0$. This implies $T(x)=T^2(w)=0$. By hypothesis $T(w)=x=0$, so $\mbox{Im }T\cap \ker T=\{0\}$.