hquang001
- 31
- 3
- Homework Statement
- A stream of elastic glass beads, each with a mass of 0.50 g, comes out of a horizontal tube at a rate of 100 per second. The beads fall a distance of to a balance pan and bounce back to their original height. How much mass must be placed in the other pan of the balance to keep the pointer at zero?
- Relevant Equations
- [tex] F = \displaystyle{\frac{\bigtriangleup{p}}{\bigtriangleup{t}}} = n.m.v [/tex]
[tex] KE_{initial} + PE_{initial} = KE_{final} + PE_{final}[/tex]
To find the mass in other pan, i need to find the force caused by beads on the pan
∴ KEinitial + PEinitial = KEfinal + PEfinal
0 + mgh = ½ mv^2
=> v = 3.13 m/s
∴ The change in momentum :
p2 - p1 = m ( v2-v1) = m( v - (-v)) = 2mv
∴ F = Δp / Δt = n. m. v
How can i apply the rate of 100 per second in this equation ?
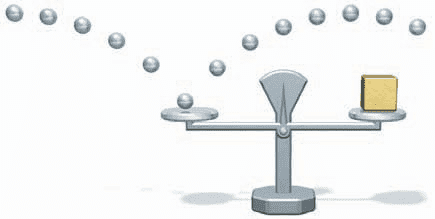
∴ KEinitial + PEinitial = KEfinal + PEfinal
0 + mgh = ½ mv^2
=> v = 3.13 m/s
∴ The change in momentum :
p2 - p1 = m ( v2-v1) = m( v - (-v)) = 2mv
∴ F = Δp / Δt = n. m. v
How can i apply the rate of 100 per second in this equation ?