[(Linear) Temporal Logic] Are the given sentences consistent or not?

[s3a]

Consider the following set of sentences that represent the requirements of a multi-threaded system for two threads t1 and t2:

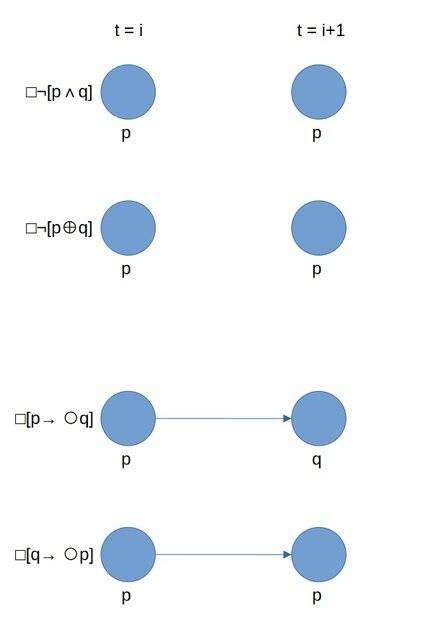
□¬[(t1 active) ∧ (t2 active)].

□[(t1 active) ⊕ (t2 active)].

□[(t1 active) → O(t2 active)].

□[(t2 active) → O(t1 active)].

(Pretend the O letters are the circles denoting the unary "next" operator.)

Could someone please let me know whether that set of sentences is consistent or not (and why)?

Any input would be GREATLY appreciated!

P.S.
Basically, if I'm correct, for a set to be consistent, there needs to be at least one case where all the statements are simultaneously true, and I think my diagram ( [link removed by Mentors]- also included as an attachment) shows such a case (but I'm not sure if I'm correct or if my diagram is even done properly). Basically, if p is true at t=i and q is true at t=i+1, then the four statements seem to hold true for me (where the bottommost one seems to be vacuously true). (If I'm correct, another case where the statements would be consistent would be if p is false and q is true, where each statement would similarly hold true, except that it would be the third statement that's vacuously true instead of the bottommost / fourth one.)

Am I correct? If not, how is this problem supposed to be solved?

In the diagram, I use p to denote "(t1 active)" and q to denote "(t2 active)".

 

[andrewkirk]

The second formula in your diagram is not consistent with the problem statement, containing a rogue additional 'not' sign.

Basically, if p is true at t=i and q is true at t=i+1, then the four statements seem to hold true for me

Not necessarily true. For instance if both t1 and t2 are always active then statement 1 fails.
You need to completely specify the state at each time, ie specify the state of both t1 and t2.
You should find it pretty easy to specify an alternating sequence that satisfies all four statements.

 

[s3a]

"The second formula in your diagram is not consistent with the problem statement, containing a rogue additional 'not' sign."
Oops! For what it's worth, here is the corrected version.:

"Not necessarily true. For instance if both t1 and t2 are always active then statement 1 fails.
You need to completely specify the state at each time, ie specify the state of both t1 and t2."
That's another oops. :D I meant to say "Basically, if p is true and q is false at t=i and p is false and q is true at t=i+1, then the four statements seem to hold true for me".

"You should find it pretty easy to specify an alternating sequence that satisfies all four statements."
There's an infinite amount of (alternating) sequences that are valid for this set of sentences where the pattern is that there are at least two moments in time, up to an unbounded maximum, and that the one thread that is active is followed by the other one thread that is active, right?

The following are correct examples, right?:
〈p,q〉
〈q,p〉
〈p,q,p〉
〈q,p,q〉
〈p,q,p,q〉
〈q,p,q,p〉

If an element of a sequence is omitted, it means that the other variable (or variables) is (or are) assumed false, right?

For example, the sequence examples above are equivalent to the following ones, right?:
〈p∧¬q,q∧¬p〉
〈q∧¬p,p∧¬q〉
〈p∧¬p,q∧¬p,p∧¬q〉
〈q∧¬p,p∧¬q,q∧¬p〉
〈p∧¬q,q∧¬p,p∧¬q,q∧¬p〉
〈q∧¬p,p∧¬q,q∧¬p,p∧¬q〉

And, then, because there is at least one example (and an infinite amount of them is at least one), we can say that the set is consistent, right?

P.S.
Sorry for saying "right?" so much. :P

 

[andrewkirk]

There are not an infinite number of structures (with the meaning given to that term by Tarski's "model theoretic" semantics - see link) that satisfy the statements. There are only two:
structure 1: $p\wedge\neg q$ for $i$ odd; $q\wedge\neg p$ for $i$ even;
structure 2: $p\wedge\neg q$ for $i$ even; $q\wedge\neg p$ for $i$ odd;
where $i$ is the time index.
All the different cases you've quoted above are just subsequences of one or the other of those.
And yes, the set of statements is consistent because there is at least one structure that satisfies it.

 

[s3a]

There are not an infinite number of structures (with the meaning given to that term by Tarski's "model theoretic" semantics - see link) that satisfy the statements. There are only two:
structure 1: $p\wedge\neg q$ for $i$ odd; $q\wedge\neg p$ for $i$ even;
structure 2: $p\wedge\neg q$ for $i$ even; $q\wedge\neg p$ for $i$ odd;
where $i$ is the time index.
All the different cases you've quoted above are just subsequences of one or the other of those.

So, there are an infinite number of sequences but only two structures (where if even an infinite amount of sequences can be expressed as part of one formula, it's one structure)?

And yes, the set of statements is consistent because there is at least one structure that satisfies it.

And, I see, thanks. :)

 

[s3a]

Also, is my (latest, corrected) diagram correct? It seems correct to me (since it seems to graphically represent both structures 1 and 2), but I'm asking just in case.

And, is it correct to say that each of the subsequences I mentioned are each not sufficient to show that the set of sentences is consistent because they don't hold for all moments in time, and in temporal logic, for a set of sentences to be consistent, they would need to hold for all (discrete) moments in time?

 

[s3a]

Actually, the sub-sequence examples I mentioned are not valid because of the third or fourth sentences (□[p → O q] or □[q → O p]), depending on whether it's p or q that's the last element of the sub-sequence, and not because it is generally the case that all moments in time need to be "occupied" in linear temporal logic, right?

As for the visualization, is this new visualization I made the correct one?:

Edit:
One thing that bothers me about the visualization above is that n seems like it can be finite, but it really should be infinite, but if I replace the n with infinity, then n-1 is still infinity, so how would I portray that?

Edit #2:
Actually, would it be a valid visualization if I were to just say t is even or odd like in the algebraic representation (the structures 1 and 2 stuff) instead of of t = whatever?

So, if instead of t = i, t =i+1, . . ., t=n-1 and t=n, would it be correct if I just wrote something like 2 ∣ t_i, 2 ∤ t_(i+1), . . ., 2 ∣ t_(n-1) and 2 ∤ t_n?

Sorry about all my questions regarding the visualization; any slides I find online all seem unclear about the visual aspects.

Could it perhaps be that these visualizations don't have a formal convention? Do they just depend on the author of the slides? That could explain why I am not finding a pattern.

 

[andrewkirk]

I searched and could not find any convention for visualisations. The writer appears free to choose their own mode of visualisation, so your visualisations are neither correct nor incorrect. Of course if your lecturer has instructed you to follow a certain convention in making visualisations, you may be correct or incorrect in your attempts to do that, but we are not in a position to comment.

FWIW I find the visualisations unhelpful as they do not give all necessary information under each blue circle. Writing just 'p' under a blue circle tells us the status of thread 1 at that time but leaves the status of thread 2 unknown. It would help the reader if you replaced all your 'p' under blue circles by $p\wedge \neg q$ and replace 'q' by $q\wedge\neg p$.

By the way, the first statement $\neg(p\wedge q)$ is redundant as it follows from the exclusive or in the second statement $p\oplus q$ (which means $(p\vee q)\wedge\neg(p\wedge q)$).

 

[s3a]

I searched and could not find any convention for visualisations. The writer appears free to choose their own mode of visualisation, so your visualisations are neither correct nor incorrect. Of course if your lecturer has instructed you to follow a certain convention in making visualisations, you may be correct or incorrect in your attempts to do that, but we are not in a position to comment.

FWIW I find the visualisations unhelpful as they do not give all necessary information under each blue circle. Writing just 'p' under a blue circle tells us the status of thread 1 at that time but leaves the status of thread 2 unknown. It would help the reader if you replaced all your 'p' under blue circles by $p\wedge \neg q$ and replace 'q' by $q\wedge\neg p$.

By the way, the first statement $\neg(p\wedge q)$ is redundant as it follows from the exclusive or in the second statement $p\oplus q$ (which means $(p\vee q)\wedge\neg(p\wedge q)$).

All right, thank you. :)

(And, sorry for the delay!)