Linear to angular acceleration of lop-sided disc

[fysiikka111]

Homework Statement

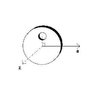
Work out the moment about the axis of a disc with off-center hole when subjected to a linear acceleration.

Homework Equations

Parallel-axis theorem

The Attempt at a Solution

Moment of inertia of offset hole:
I_oh=I_h+mr^2
where I_h is MoI of hole about its center, m is mass of hole, and r is offset radius.

MoI of half-disc (semicircle) with offset hole:
I_dh=((MR^2)/4)-I_oh
where M is mass of half-disc without hole, and R is radius of disc.

Difference in MoI between half-disc with hole and half-disc without hole:
I_diff=((MR^2)/4)-I_dh

If the disc is accelerating as in the diagram (where a is linear acceleration and z the axis of rotation of the disc), how does a translate into angular acceleration of the disc? Is there a site that explains something similar to this?
Thanks

 

[fysiikka111]

I am trying to model an accelerometer.
The discs' shaft is connected to a coil spring, so the angular displacement of the disc relates to the acceleration of the casing.

 

[ideasrule]

This problem is easier to solve using the accelerating reference frame than using the inertial frame. In the accelerating frame, the disc behaves exactly as if it were in a gravitational field with g=a.

You can model the disc as a combination of a solid disc, and a smaller disc with negative mass. "Gravity" applies a force to the negative mass, which in turn applies a torque about the axis. Gravity applies no torque to the solid disc itself because it's perfectly symmetrical. You also have to consider the effect of the negative mass on the moment of inertia, which is easy: you just add the moments of inertia of the two discs.

 

[fysiikka111]

Are my calculations of the MoI's in the first post correct? I am not sure, however, how to use the MoI as its not an angular acceleration that is acting on the disc, but a linear one. So, how do I calculate the effect of the linear acceleration on the rotation of the disc? One way would be to integrate over the area of the half-disc with hole to find the total torque each particle exerts due to an acceleration a of the casing:
F=ma
T=Fd
Total T=integral of T
However, the integral is hard because the shape is somewhat irregular. Although it should be possible to do it with a double integral using a polar coordinate system.
Is there an easier way though, using the MoI?

 

[ideasrule]

I'm actually confused about your calculations in the first post, and why you're considering half-discs. This equation:

I_oh=I_h+mr^2

is correct. Since I_h=1/2*mb^2 where b is the radius of the hole, the total moment of inertia is I_oh=m(1/2*b²+r²).

However, the integral is hard because the shape is somewhat irregular. Although it should be possible to do it with a double integral using a polar coordinate system.
Is there an easier way though, using the MoI?

That's why I suggested calculating the force exerted by "gravity" (acceleration) on a small disc with negative mass. Gravity always acts through the center of mass, which is just the center of the disc. Since this gravity acts perpendicular to the line between the center of the large disc and the center of the hole, torque is just ma*(center-to-center distance).

 

[fysiikka111]

Gravity always acts through the center of mass, which is just the center of the disc. Since this gravity acts perpendicular to the line between the center of the large disc and the center of the hole, torque is just ma*(center-to-center distance).

So the disc can be ignored and just the imbalance caused by the hole be calculated. Hence, torque at axis is
T=mad
where m is negative mass of hole, and d distance between center of disc to center of hole. Isn't this only an approximation though because the hole isn't a point mass - i.e. the torque produced by the parts of the hole that are farther away from the axis are greater than the parts that are closer to it. How would I take that into account?