- #1
Ivan Antunovic
- 111
- 4
Homework Statement
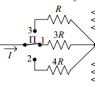
For the network of constant current shown in Figure 4 it is known that R1 = 50 Ω and , R = 10 Ω. When the switch P is
in the 1-position , current I = 50 mA and Ip = 70 mA known i . When the switch P is in
the 2-position , current I' = 40 mA and Ip' = 90 mA are known . Determine the current Ip''
when the switch switches to the third position.
Homework Equations
The Attempt at a Solution
By linearity and superposition theorem we have a linear network and if we have our active load network we can write I = xU + y , where current I is the response and voltage U represents excitation , constants x and y are determined by the resistance of the active network ,where x has dimension of A/V and y has dimension of A.
By solving equation 1 and equation 2 I get that,
x = 0.2 and y = -0.23,
for the 3rd equation I get:
Ip" = xU1 + y = 0.2 U1 - 0.23
I have two unknowns Ip" ,U1 and only 1 equation.
What am I doing wrong?