Link between Z-transform and Taylor series expansion

[fatpotato]

Homework Statement

Inverting a Z-transform using Taylor series expansion

Relevant Equations

See embedded image in my post

Hello,

I am reading a course on signal processing involving the Z-transform, and I just read something that leaves me confused.

Let $F(z)$ be the given Z-transform of a numerical function $f[n]$ (discrete amplitudes, discrete variable), which has a positive semi-finite support and finite ROC. My textbook says that we should be able to compute the inverse Z-transform of $F(z)$, so the $f[n]$ values, using the fact that "$f[n]$ values are given by the Taylor series expansion of $z^{-n_0} F(z^{-1})$ around $z=0$", using the following equation:

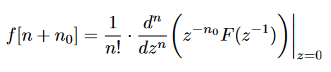
This sounds fascinating, but I don't understand! How are Z-transform and Taylor series expansion linked, and why? I only ever learned about inverting the Z-transform using tables, long division or using the inverse transform definition involving contour integral in the complex plane (which I never had the chance to use).

Any information is welcome!

 

[pasmith]

Look at the definition: $$F(z) = \sum_{n=0}^\infty f[n]z^{-n}$$ Setting $t = z^{-1}$ this is $$F(t^{-1}) = \sum_{n=0}^\infty f[n]t^{n}.$$ This is a power series in $t$, so if $G(t) = F(t^{-1})$ has a convergent Taylor series at 0 this is $$\sum_{n=0}^\infty f[n]t^{n} = \sum_{n=0}^\infty \frac{1}{n!} G^{(n)}(0)t^n$$ and hence $$f[n] = \frac{1}{n!} G^{(n)}(0) = \frac{1}{n!}\left.\frac{d^n}{dt^n}F(t^{-1})\right|_{t=0}.$$

 

[fatpotato]

Beautiful, thank you for the derivation!

In a classical engineering program setting, I tend to believe that applying Taylor series would be limited to Calculus and I would have never thought of using it here.

Would you happen to have a suggestion on where I can expand my horizons to come up with such reasonings myself?