Linking of Curves: C1, C2 in R^3, D1, D2, Finite Loops

[wofsy]

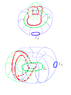
Take two closed loops,C1 and C2, in R^3 that do not intersect and whose linking number is zero.

Chose two manifolds D1 and D2 whose boundaries are C1 and C2 and which intersect in their interiors transversally and do not intersect anywhere along their boundaries.

The intersection is a finite collection of new closed loops. Can anyone of these have non-zero linking number with C1 or C2?

I don't think so but...

 

[zhentil]

Hi Wofsy,

The intersection is not necessarily a finite collection of new closed loops, even if the intersection is transverse. For the sake of argument, though, let's assume it is. Then the question is whether two circles in the same disk can have non-zero linking number. One of the characterizations of zero linking number is that one circle bounds a disk in the complement of the other. But then it's obvious.

 

[wofsy]

Hi Wofsy,

The intersection is not necessarily a finite collection of new closed loops, even if the intersection is transverse. For the sake of argument, though, let's assume it is. Then the question is whether two circles in the same disk can have non-zero linking number. One of the characterizations of zero linking number is that one circle bounds a disk in the complement of the other. But then it's obvious.

Why is the intersection not a collection of closed loops?

I did not imagine that the loops bounded disks. The surfaces could have handles.

 

[zhentil]

Two disks which intersect transversally can intersect in a line segment. It's only true that the intersection would be loops if the surfaces had no boundary.

For the second part, I'll have to think a little bit. I thought you meant that D1 and D2 were disks.

 

[wofsy]

Two disks which intersect transversally can intersect in a line segment. It's only true that the intersection would be loops if the surfaces had no boundary.

For the second part, I'll have to think a little bit. I thought you meant that D1 and D2 were disks.

Right - I meant to say that they do not intersect along their boundaries - only in the interiors.

I think I understand how to do this now but do not have a tight proof.

Boundary intersections - I think - can be eliminated by adding handles to one disk that surround segments of the boundary of the other. When you are done adding handles the two original loops now bound two discs with some handles attached and these two new surfaces with handles do not intersect anywhere along their boundaries. These handles can not create links for the theorem to be true.

 

[Ben Niehoff]

I think I found an example, if I've interpreted your post correctly. It's hard to describe, so I drew a picture. Hope it uploads properly. The curve C1 is in green, as is the manifold D1. The curve C2 and manifold D2 are in blue. The intersection is in red.

The surface D1 is non-orientable. I think this is the only way to get it to work. The red curve links C1 twice, basically interweaving a figure-8 on the circle.

D2 is a torus with a hole cut out, bounding C2. D1 is a Klein bottle with a hole cut out, bounding C1.

 

[Ben Niehoff]

If you allow the surfaces to have self-intersections (but no intersection with either its own boundary, or the other surface's boundary), then I can find a solution with orientable surfaces. And with linking number 1 instead of 2.