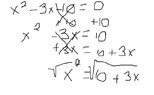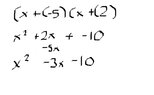OMGMathPLS
- 64
- 0
List all values of x for which each rational expression is undefined:
$$\frac{x^2-9}{x^2-3x-10}$$
Answer is 3, -3
q1) Are these -, and positive answer interchangeable ones because it is a rational expression so when I see rational that's going to signal it's going to need 2 answers (either positive or negative) or is it the list all values that clues me in? Or is the word undefined?
q2) And then to actually solve it. How do I start reducing or icing the individual variables out when it's in a fraction? I'm really sorry if I sound ignorant. Since there's no = sign I'm not sure how to do it over a fraction. Thanks if anyone can help.
$$\frac{x^2-9}{x^2-3x-10}$$
Answer is 3, -3
q1) Are these -, and positive answer interchangeable ones because it is a rational expression so when I see rational that's going to signal it's going to need 2 answers (either positive or negative) or is it the list all values that clues me in? Or is the word undefined?
q2) And then to actually solve it. How do I start reducing or icing the individual variables out when it's in a fraction? I'm really sorry if I sound ignorant. Since there's no = sign I'm not sure how to do it over a fraction. Thanks if anyone can help.
Last edited by a moderator: