Locating the centre of mass of an object?

[joedirt]

Homework Statement

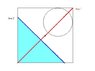
A square of side 2R has a circular hole of radius R/2 removed from one quarter (see file attachment). The
centre of the hole is located at (R/2, R/2) from the centre. Locate the centre of mass with respect to the centre of the square.

Homework Equations

The Attempt at a Solution

I'm new to this topic and have no idea where to start with this problem. I have other questions similar to this so relevant equations and the solution would be much appreciated!

 

[Moorebc]

I'm not familiar with how you are "supposed" to solve this, but here are my thoughts. If I look for two lines where, for each, the distribution of mass is equal on either side, the COM will be located the intersection of them.

The first one is easy as there is an axis of symmetry running from the southwest corner to the northeast one, through the center of the plate (and the center of the hole).

Now we can look for a second line, perpendicular to the first, running NW - SE. This will be located parallel to and slightly below and left of the line connecting the NW and SE corners. That defines a triangle of solid plate at lower left and an upper right shape containing the hole. Then, for equal mass distribution either side of this line, the mass (read area) of the triangle MUST to be equal to half the area of the whole figure. So all you have to do is to calculate the altitude of this triangle with respect to the hypotenuse then you can calculate the distance of the intersection point from the center of the square.


Edit - here's a diagram to make things clearer

 

[vela]

I'm new to this topic and have no idea where to start with this problem. I have other questions similar to this so relevant equations and the solution would be much appreciated!

It's against the forum rules to provide solutions. You need to work through the problem yourself.

If you really have no idea how to even start the problem, you need to review your notes and study the relevant sections of your textbook.

 

[Filip Larsen]

There are many ways you can solve this. You can follow Varialectios suggestion and use symmetry, you can find a way to divide your object up into smaller parts where you can easily calculate the mass and center of mass of each part and then combine those parts back to a common center of mass, and you can even start with a full square and then "subtract" the hole.

 

[pongo38]

Go back to the definition of centre of mass, which refers not to equal masses but to the algebraic sum of the first moments of area being zero. Where is the origin such that a1.y1-a2.y2 =0 etc ?