Locus of Incentre Problem: Find Ellipse

[Saitama]

Problem:
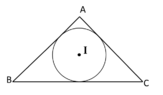
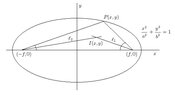
Given the base of a triangle and sum of its sides, then the locus of the centre of its incircle is:

A)straight line
B)circle
C)ellipse
D)hyperbola

Attempt:
Since the given answer is ellipse, I tried showing that the sum of the distances of incentre from the end points of base is constant.

The side lengths opposite to vertex A, B and C are a, b and c respectively. As per the question, a (base) and a+b+c is given. The distance IB is $r/\sin(B/2)$ and IC is $r/\sin(C/2)$, where $r$ is the radius of incircle. Hence,

$$IB+IC=r\left(\frac{1}{\sin(B/2)}+\frac{1}{\sin(C/2)}\right)\,\,\,\, (*)$$
I use the following formulas:
$$r=\frac{\Delta}{s}=\sqrt{\frac{(s-a)(s-b)(s-c)}{s}}$$
$$\sin\left(\frac{B}{2}\right)=\sqrt{\frac{(s-a)(s-c)}{ac}}$$
$$\sin\left(\frac{C}{2}\right)=\sqrt{\frac{(s-a)(s-b)}{ab}}$$
Substituting in (*) and simplifying,
$$IB+IC=\sqrt{\frac{a}{s}}\left(\sqrt{c(s-b)}+\sqrt{b(s-c)}\right)$$
The terms outside the parentheses is constant, I am unable to prove that the terms inside the parentheses are a constant too. :(

Any help is appreciated. Thanks!

 

[Opalg]

This is an interesting problem. The points $B$ and $C$ are fixed, and the triangle $ABC$ has a constant perimeter. So the point $A$ must lie on an ellipse with foci at $B$ and $C$. The incentre $I$ also lies on an ellipse, but the foci of that ellipse are not at $B$ and $C$, so you should not expect $\overline{IB} + \overline{IC}$ to be constant.

The only way I can solve the problem is to use coordinate geometry. Let $A$ be the point $(a\cos\theta,b\sin\theta)$, so that \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) is the ellipse on which $A$ lies. Then $B$ and $C$ are the foci of that ellipse, with coordinates $B = (-ae,0)$, $C = (ae,0)$, where $e$ is the eccentricity of the ellipse, given by $b^2 = a^2(1-e^2)$. The lengths of the sides of the triangle are $\overline{BC} = 2ae$, $\overline{CA} = a(1-e\cos\theta)$, $\overline{AB} = a(1+e\cos\theta)$.

I then used a very useful formula for the coordinates of the incentre that I found here. In words, it says that you take the coordinates of the three vertices of the triangle, multiply each of them by the length of the opposite side, add them, and finally divide by the perimeter of the triangle. I leave you to apply that formula to our triangle here. I found that it gives $I = \Bigl(ae\cos\theta, \dfrac{be\sin\theta}{1+e}\Bigr).$ Thus $I$ lies on the ellipse \(\displaystyle \frac{x^2}{a^2e^2} + \frac{(1+e)^2y^2}{b^2e^2} = 1\), which passes through the points $B$ and $C$ (and so certainly does not have its foci at those points).

 

[MarkFL]

Like Opalg, I found this problem interesting and find a coordinate geometry approach to be the most straightforward.

I decided to orient the fixed base of the triangle along the $x$-axis whose center is at the origin, and let its length be $2f$. From the definition of an ellipse, we know the locus of the movable vertex is an ellipse, which I describe by:

\(\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)

Please refer to the following diagram:

View attachment 1857

Point $P$ is an arbitrary point on the ellipse, and point $I$ is the associated incenter. It is the intersection of the two angle bisectors $\ell_1$ and $\ell_2$.

Let's parametrize point $P$ as follows:

\(\displaystyle x(t)=t\)

\(\displaystyle y(t)=\frac{b}{a}\sqrt{a^2-t^2}\)

where \(\displaystyle -a\le t\le a\)

While we are only considering the top half of the ellipse here, a similar argument could be used for the bottom half.

For these two lines, we know they pass through the foci of the ellipse, so we need to determine their slopes.

For line $\ell_1$, let's first look at the slope of the line through the points:

\(\displaystyle \left(t,\frac{b}{a}\sqrt{a^2-t^2} \right)\) and \(\displaystyle (f,0)\)

It's angle of inclination is therefore:

\(\displaystyle \theta_1=\tan^{-1}\left(\frac{b\sqrt{a^2-t^2}}{a(t-f)} \right)\) where \(\displaystyle t\ne f\)

And so the angle of inclination of $\ell_1$ is:

\(\displaystyle \frac{\theta_1}{2}=\frac{1}{2}\tan^{-1}\left(\frac{b\sqrt{a^2-t^2}}{a(t-f)} \right)\)

Hence, the slope of $\ell_1$ is found using a half-angle identity for tangent:

\(\displaystyle m_1=\frac{\sin\left(\tan^{-1}\left(\dfrac{b\sqrt{a^2-t^2}}{a(t-f)} \right) \right)}{1+\cos\left(\tan^{-1}\left(\dfrac{b\sqrt{a^2-t^2}}{a(t-f)} \right) \right)}\)

Using the fact that \(\displaystyle f^2=a^2-b^2\) we find:

\(\displaystyle m_1=-\frac{b}{a+f}\sqrt{\frac{a+t}{a-t}}\)

Armed now with the slope and the point through which it passes, line $\ell_1$ is given by (using the point-slope formula):

\(\displaystyle y=\frac{b}{a+f}\sqrt{\frac{a+t}{a-t}}(f-x)\)

For line $\ell_2$, let's first look at the slope of the line through the points:

\(\displaystyle \left(t,\frac{b}{a}\sqrt{a^2-t^2} \right)\) and \(\displaystyle (-f,0)\)

It's angle of inclination is therefore:

\(\displaystyle \theta_2=\tan^{-1}\left(\frac{b\sqrt{a^2-t^2}}{a(t+f)} \right)\) where \(\displaystyle t\ne -f\)

And so the angle of inclination of $\ell_2$ is:

\(\displaystyle \frac{\theta_2}{2}=\frac{1}{2}\tan^{-1}\left(\frac{b\sqrt{a^2-t^2}}{a(t+f)} \right)\)

Hence, the slope of $\ell_2$ is found using a half-angle identity for tangent:

\(\displaystyle m_2=\frac{\sin\left(\tan^{-1}\left(\dfrac{b\sqrt{a^2-t^2}}{a(t+f)} \right) \right)}{1+\cos\left(\tan^{-1}\left(\dfrac{b\sqrt{a^2-t^2}}{a(t+f)} \right) \right)}\)

Using the fact that \(\displaystyle f^2=a^2-b^2\) we find:

\(\displaystyle m_2=\frac{b}{a+f}\sqrt{\frac{a-t}{a+t}}\)

Armed now with the slope and the point through which it passes, line $\ell_2$ is given by (using the point-slope formula):

\(\displaystyle y=\frac{b}{a+f}\sqrt{\frac{a-t}{a+t}}(x+f)\)

Equating the two lines, and solving for $x$, we find:

\(\displaystyle =\frac{b}{a+f}\sqrt{\frac{a+t}{a-t}}(f-x)=\frac{b}{a+f}\sqrt{\frac{a-t}{a+t}}(x+f)\)

\(\displaystyle (a+t)(f-x)=(a-t)(x+f)\)

\(\displaystyle af-ax+ft-tx=ax+af-tx-ft\)

\(\displaystyle ft=ax\implies x=\frac{f}{a}t\implies y=\frac{b}{a+f}\sqrt{f^2-x^2}\)

Squaring this value for $y$, (which gives us the bottom half) we obtain the locus for $I$:

\(\displaystyle \frac{x^2}{f^2}+\frac{y^2}{\left(\dfrac{bf}{a+f} \right)^2}=1\)

which is clearly an ellipse.

 

[Saitama]

Hi Opalg and MarkFL! :)

Thank you both for your helpful solutions. I prefer to stay with parametric coordinates used by Opalg. :P

It was very silly of me to consider B and C as the foci.

About that incentre formula, it is also in my course and I need to memorise that (Doh).

Thank you once again.

 

[CellCoree]

Hello,

Thank you for your attempt at solving this problem. It seems like you are on the right track, but there is a simpler way to prove that the locus of the incentre is an ellipse.

First, let's define the coordinates of the vertices of the triangle as A(0,0), B(a,0), and C(c,d). We can assume that the base of the triangle is on the x-axis, and the coordinates of the vertex C are (c,d) since the sum of the sides is given.

Next, let's find the coordinates of the incentre, I. We know that the incentre is the intersection of the angle bisectors of the triangle, which can be written as the equations:

$$y=\frac{dx}{c}$$
$$y=-\frac{d}{a-c}(x-a)$$

Solving these equations, we get the coordinates of the incentre as:

$$I\left(\frac{ac}{a+c},\frac{ad}{a+c}\right)$$

Now, let's find the distance of the incentre from the end points of the base, A(0,0) and B(a,0):

$$AI=\sqrt{\left(\frac{ac}{a+c}\right)^2+\left(\frac{ad}{a+c}\right)^2}=\frac{a\sqrt{c^2+d^2}}{a+c}$$

$$BI=\sqrt{\left(a-\frac{ac}{a+c}\right)^2+\left(\frac{ad}{a+c}\right)^2}=\frac{a\sqrt{c^2+d^2}}{a+c}$$

We can see that the sum of these distances is a constant, $a\sqrt{c^2+d^2}/(a+c)$, which proves that the locus of the incentre is an ellipse with foci at A and B and major axis of length a+c.

I hope this helps. Let me know if you have any further questions.