Looking for a trajectory integrator that also supports cubic potential

[Cleonis]

TL;DR Summary

Looking for a trajectory integrator that also supports cubic potential, in order to corroborate a trajectory found with an interactive diagram that implements in numerical analysis form Hamilton's stationary action.

The context:
I created an educational resource, a set of interactive diagrams that allow the user to see how Hamilton's stationary action arrrives at the true trajectory. There is a diagram for each of the following three cases:

- Uniform force, hence the potential increases linear with position
- Hooke's law, hence the potential increases quadratic with displacement
- Force increases quadratic with displacement, hence the potential increases with the cube of the displacement.

In each of the three instances the start point is t=-1, height zero, the end point is t=1, height zero.

The total time of 2 units of time is divided in 20 sub-sections, the nodes can be moved with sliders. The sliders modify the ascending part of the trajectory, the descending part is a mirror of the ascending part.

The screenshots below are excepts of the full diagrams. The full diagrams have 4 subpanels. The subpanels not shown here are the subpanel that contains the controlling sliders, and the subpanel displaying the value of Hamilton's action.

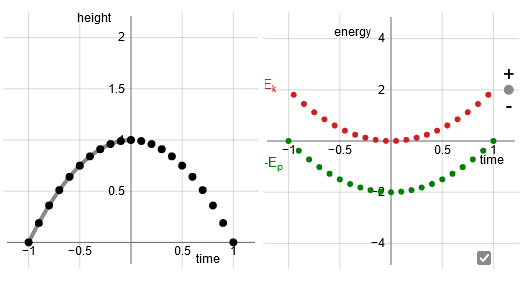
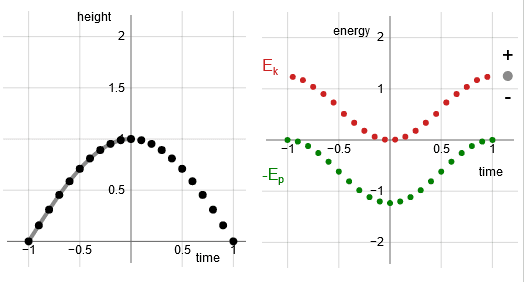
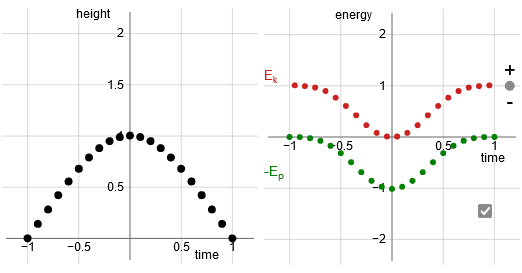
As we know, with a linear potential the resulting trajectory is a parabola, and with Hooke's law the resulting motion is harmonic oscillation. The diagrams show that indeed those trajectories correspond to stationary action.

In the case of a potential that increases with the cube of the displacement there is (to my knowledge) no analytic solution. So in that case I used the interactive diagram to find the corresponding trajectory.

I would like to show independent corroboration of that trajectory.

I'm confident that the interactive diagram is good.

The red and green dots in the righthand subpanel show the energy.
(Kinetic energy: red dots. The curve for the potential energy has been flipped upside down; the green dots represent the minus potential energy. With the potential energy curve upside down there is a visual verification. The true trajectory has the property that at every point in time the rate of change of kinetic energy matches the rate of change of potential energy. With the curve for the potential energy upside down the red and green curve are parallel to each other all the time.)
My question:
I have been looking whether there is an online trajectory integrator that will take any potential as input, so that I can input a potential that increases with the cube of displacement. All the online trajectory integrators I looked at are for one case only: Earth gravity.

Of course, I can implement such an integrator myself, but for corroboration: the more independent the more convincing.

Does anyone know such an integrator is available somewhere?

 

[hilbert2]

Try, for example, this one which uses 4th order Runge-Kutta integration

https://keisan.casio.com/exec/system/1548128854

and set F(x,y,p) = -sign(y)*y^2. This is equivalent to a system with a dimensionless equation of motion

$\displaystyle m\frac{d^2 y}{dt^2} = -sign(y)y^2$

and mass $m=1$, where the force depends on the square of the position coordinate and is always directed towards the equilibrium point. Set x₀ = y₀ = 0 and y₀' = 1, to make the particle begin from the equilibrium point y = 0 with an initial velocity directed to the right. If you make the force depend on a higher power of $y$, such as $F\propto y^{10}$, you will notice that the graph of the trajectory $y(t)$ will begin to look more like a sawtooth graph where the particle/object is bouncing between two hard walls.

 

[Ibix]

Python's scipy.integrate integrates arbitrary differential equations.

 

[Cleonis]

Try, for example, this one which uses 4th order Runge-Kutta integration
https://keisan.casio.com/exec/system/1548128854

Thank you.

I used the following settings:
The function to be Runge-Kutta integrated: -sign(y)*3*y^2
Initial slope: 1.38
Partition number: 20

In the (manual) numerical analysis implementation of stationary action the potential was set to y^3
Differentiating with respect to y gives 3*y^2 for the function to be integrated.

I tweaked the initial slope until I had a trajectory that is back to height zero at t=1

The Runge-Kutta integration shows that with those settings the trajectory does not climb all the way to y=1.0, reaching 0.984 instead.

In the manual numerical analysis implementation it looked so close that I assumed that it actually does climb to y=1.0, and from there I adjusted the rest to get the curves for the energies to be visually parallel.

In the screenshot above the first column is the result of the Runge-Kutta integration, the second column is the values for the nodes that I had arrived at using the diagram itself, the third column is the difference between the two.

 

[hilbert2]

I used the following settings:
The function to be Runge-Kutta integrated: -sign(y)*3*y^2
Initial slope: 1.38
Partition number: 20

It's better to have a larger partition number, like 500, to have a smaller time step and more accurate result.

 

[Cleonis]

It's better to have a larger partition number, like 500, to have a smaller time step and more accurate result.

Well, in this particular case the purpose is to corroborate a manual approximation of the trajectory, so the accuracy requirement is very low.

I tried the same settings, with partition number 200 (instead of 20). The trajectory reaches the same height, to within 0.00001
So: the RK-4th-order performance with partition number 20 is more than sufficient.

 

[Cleonis]

Try, for example, this one which uses 4th order Runge-Kutta integration

For completeness let me show what is interesting about the classes of cases where the potential increases with the cube (or higher power) of the displacement.

The frames of the animated GIF are successive screenshots of an interactive diagram.

In the lower right subpanel:
Red dot: integral of the kinetic energy
Green dot: integral of the minus potential energy
Blue dot: Hamilton's action

The main slider sweeps out variation of the trial trajectory.
The true trajectory has the property that the rate of change of kinetic energy matches the rate of change of potential energy the entire time.

Since kinetic energy is proportional to the square of velocity: when the height of the trial trajectory is changed the change of the integral of the kinetic energy is in quadratic proportion to that.

The diagram here is for the case where the potential energy increases with the cube of the displacement. So: when the height of the trial trajectory is changed the change of the integral of the potential energy is proportional to the cube of the displacement.

This means that in this diagram the change in (integral of) the potential energy is larger than the change in (integral of ) the kinetic energy. Phrased differently: the response of the potential energy to variation of the trial trajectory outpaces the response of the kinetic energy.

In the case of cubic (and higher power) potential: at the point where the trial trajectory coincides with the true trajectory the value of Hamilton's action is at a maximum.

This hammers home the point that in the case of Hamilton's stationary action the decisive criterion is that the derivative of Hamilton's action is zero.

Whether the point of zero derivative is a minimum or a maximum is immaterial. The property that counts is that the derivative of Hamilton's action is zero.The difference between the names 'least action' and 'stationary action' is not a technicality; it is fundamental. Stationary action is inherently about looking for that one trial trajectory such that the derivative of Hamilton's action is zero.