Loop the Loop Problem Solution | N > 0, Energy Conservation Method

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

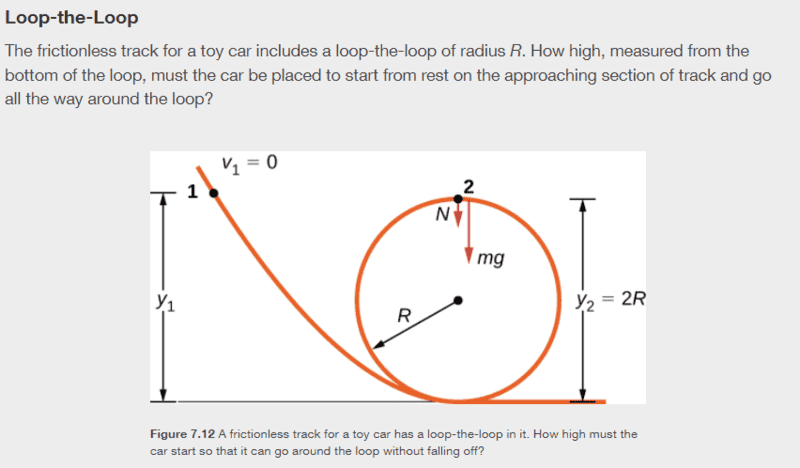
The solution is,

Does someone please know why $N > 0$. I though at the min speed to still go around the loop, we could set $N = 0$ and $mg$ provides the centripetal force.

Also, I am wondering how to do this problem with using energy conservation.

My working is
$N + mg = \frac{mv^2}{R}$
$mgy_1 = mgy_2 + \frac{1}{2}mv^2$
$mgy_1 = 2mgR + \frac{R(N + mg)}{2}$
$y_1 = 2R + \frac{R(N + mg)}{2mg}$
$y_1 = R(\frac{N}{2mg} + \frac{5}{2})$

However, I am not to sure how to go from here. If I assume that $N = 0$ I get $y_1 = \frac{5R}{2}$ so any height greater than or equal to $y_1$ the object should loop the loop?

Many thanks!

 

[erobz]

Does someone please know why $N > 0$. I though at the min speed to still go around the loop, we could set $N = 0$ and $mg$ provides the centripetal force.

What happens to $N$ if we start at higher than $y = \frac{5R}{2}$?

If you are just asking about the criterion $N>0$, because at $N=0$ it has lost contact with the track.

 

[kuruman]

Also, I am wondering how to do this problem without using energy conservation.

My working is
$N + mg = \frac{mv^2}{R}$
$\color{red}{mgy_1 = mgy_2 + \frac{1}{2}mv^2}$
$mgy_1 = 2mgR + \frac{R(N + mg)}{2}$
$y_1 = 2R + \frac{R(N + mg)}{2mg}$
$y_1 = R(\frac{N}{2mg} + \frac{5}{2})$

However, I am not to sure how to go from here. If I assume that $N = 0$ I get $y_1 = \frac{5R}{2}$ so any height greater than or equal to $y_1$ the object should loop the loop?

Many thanks!

If you want to solve the problem without using energy conservation, you cannot use the equation in red which expresses energy conservation. You have to solve Newton's second law equation for the trajectory. I don;t think it can be done analytically. That is why you use energy conservation.

 

[member 731016]

Thank you for your replies @erobz and @kuruman!

Yes sorry there was a typo in the Post #1. I was asking how to solve this problem using energy conservation.

Many thanks!

 

[kuruman]

The solution that you posted uses energy conservation (first equation). Take a good look at it.

 

[member 731016]

What happens to $N$ if we start at higher than $y = \frac{5R}{2}$?

If you are just asking about the criterion $N>0$, because at $N=0$ it has lost contact with the track.

Thank you for your reply @erobz!

If we start a very small increment little higher than y_1 then $N$ could be $0.00000001N$

Many thanks!

 

[member 731016]

The solution that you posted uses energy conservation (first equation). Take a good look at it.

True! Thank you @kuruman!

 

[jbriggs444]

If you are just asking about the criterion $N>0$, because at $N=0$ it has lost contact with the track.

No experiment can distinguish reliably between $N>0$ and $N \ge 0$. So as a question about physics, the distinctiont is irrelevant.

However, putting on my mathematician's hat, the correct statement is that at [calculated] $N < 0$ it has lost contact with the track. At $N=0$ the trajectory of the ball is neither accelerating into the track nor accelerating away from the track. It is maintaining zero separation. Zero separation is the criterion I would use for "in contact".

 

[member 731016]

No experiment can distinguish reliably between $N>0$ and $N \ge 0$. So as a question about physics, the distinctiont is irrelevant.

However, putting on my mathematician's hat, the correct statement is that at [calculated] $N < 0$ it has lost contact with the track. At $N=0$ the trajectory of the ball is neither accelerating into the track nor accelerating away from the track. It is maintaining zero separation. Zero separation is the criterion I would use for "in contact".

Thank you for your help @jbriggs444 ! That is very helpful!