- #1
CarsonAdams
- 15
- 0
What is the formula to evaluate Lorentz force on a curved current carrying wire in a non-constant magnetic field (given by some known vector field). The standard form of Lorentz force (Fb=BxlI) when B and the wire's length 'l' are constants does not account for this case, nor does the differential form of the equation when the wire can be curved but the magnetic force must be constant (dFb=(Bxdl)I).
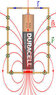
For example, if B is being generated by a simplified dipole and the curve is being generated by some parameterized function, what integral describes the force exerted on the wire? (This is shown below with the wire being a circular loop centered on the dipole. Though this is possibly a trivially symmetrical case that evaluates to zero, its still worth considering.)
My initial guess is that such an evaluation needs to be done using some sort of line integral or at least a double integral, but the cross product throws the whole thing off for me. Suggestions or known properties?
(This is in conjunction with an effort to create a quantitative analysis of homopolar motors, two of which with slightly different parameters and properties from the above question are shown below)
For example, if B is being generated by a simplified dipole and the curve is being generated by some parameterized function, what integral describes the force exerted on the wire? (This is shown below with the wire being a circular loop centered on the dipole. Though this is possibly a trivially symmetrical case that evaluates to zero, its still worth considering.)
My initial guess is that such an evaluation needs to be done using some sort of line integral or at least a double integral, but the cross product throws the whole thing off for me. Suggestions or known properties?
(This is in conjunction with an effort to create a quantitative analysis of homopolar motors, two of which with slightly different parameters and properties from the above question are shown below)