Lorentz Transformation Equations, time transformation

[Dale]

@Grimble

It may help you to draw the lines t=0, t=1, t=2, and x=0, x=1, x=2 on a spacetime diagram for K'. That was one of the key exercises that I did learning SR. The easiest way to do it is to write them as parametric equations and do substitution.

 

[ghwellsjr]

OK. I did not make it clear, but when I wrote:

"So for an event at t = 15, x = 9, in system K, where system K' is traveling along the x-axis at velocity 0.6c, γ = 1.25. (Origin of system K, (t,x,y,z), (0,0,0,0); Origin of system K', (10, 6,0,0))"

that I was referring to the coordinates of the Origin of 0' in the reference frame of system K.
So that starting from the origin of 0, that is (0,0,0,0), system K' (it's origin specifically) has traveled along the common x-axis for 10 seconds at 0.6c or 6 light seconds, arriving at (10,6,0,0). Which are the coordinates for the event at (10,6,0,0) in frame K, which is the same event that has coordinates (10,6,0,0) in frame K'.

The coordinates of the origin of system K' in system K are x' = γ(x - vt) = 1.25(6 - 10(0.6) = 0, and t' = 1.25(10 - 6(0.6)) = 8
while the coordinates after another 5 seconds when t = 15, x = 9 would be, x' = 1.25(9 - 15(0.6)) = 0 and t' = 1.25(15 - 9(0.6)) = 12

So the value calculated for the time coordinate, t' is fine = t/γ, whereas the x' coordinate always comes out at 0.
But it still seems reasonable to me that the x' coordinate is a function of the x coordinate γx, LESS the displacement of the O' frame when x' = 0.

As near as I can tell, you are describing an object "O" that is traveling at 0.6c in system K and passes through its origin. Here is a spacetime diagram depicting this scenario:

The origin of K is the black dot. The two events you specified are shown in green and red.

Now we transform all the dots to system K':

Notice how the origin of K' is still at (0,0,0,0,) and the other events transform as you calculated.

 

[Grimble]

Which are the coordinates for the event at (10,6,0,0) in frame K, which is the same event that has coordinates (10,6,0,0) in frame K'.

This should of course have read: "... which is the same event that has coordinates (0,0,0,0) in frame K'. "
Apologies for poor reviewing before posting.

 

[Grimble]

AAAAHHH! Now I have it!

I was as mentioned above still stuck in the rut of Galileian relativity!
It does in fact work just as you say it works. I was failing to grasp that while,the Origin of K' is an event at a fixed location in system K - (10,6,0,0) - the location of it, its spatial coordinates are constantly changing as that frame moves in system K. It moves as a function of the time t. So the x coordinate increases as a function of the time t. That function being -vt.
So I can see how it all works now.
If we take a spaceship 0.01ly in length where the rear is at (10,6,0,0) then the front would be at (10,6.01,0,0). And in system K' the front would have the coordinates
x' = 1.25(6.01 - 10(0.6)) = 0.0125 while t' would be t' = 1.25(10 - (6.01)(0.6)) = 7.9925 so the front would be 0.0075seconds in time reaching that point before the rear of the train reached (10,6,0,0)?

 

[ghwellsjr]

AAAAHHH! Now I have it!

I was as mentioned above still stuck in the rut of Galileian relativity!
It does in fact work just as you say it works. I was failing to grasp that while,the Origin of K' is an event at a fixed location in system K - (10,6,0,0) - the location of it, its spatial coordinates are constantly changing as that frame moves in system K. It moves as a function of the time t. So the x coordinate increases as a function of the time t. That function being -vt.
So I can see how it all works now.

How many times do you have to be told that the Origin of every system has the coordinates (0,0,0,0)? The origin, like all other events, doesn't move. Its spatial coordinates don't change. They remain all zeroes. If you are talking about an object or observer which passes through the origin of a system, its spatial coordinates can change with time in any arbitrary manner that you want. You can describe its motion as any function of time that you desire and then you can transform the coordinates of any events along its worldline to see how the coordinates appear in another system moving with respect to the original system. That's what I did for you in post #37. The motion of a frame is independent of the motion of any object or observer.

If we take a spaceship 0.01ly in length where the rear is at (10,6,0,0) then the front would be at (10,6.01,0,0). And in system K' the front would have the coordinates
x' = 1.25(6.01 - 10(0.6)) = 0.0125 while t' would be t' = 1.25(10 - (6.01)(0.6)) = 7.9925 so the front would be 0.0075seconds in time reaching that point before the rear of the train reached (10,6,0,0)?

Are you trying to understand Length Contraction with this example? If so, you are taking the wrong approach. If not, what are you trying to do?

Also, please spend some time proofing your posts. You started out with a spaceship and ended up with a train!

 

[Grimble]

How many times do you have to be told that the Origin of every system has the coordinates (0,0,0,0)? The origin, like all other events, doesn't move. Its spatial coordinates don't change. They remain all zeroes.

And that is EXACTLY what I said! The location of frame K', its origin will be moving in system K'. BECAUSE IT IS A MOVING FRAME in system K, the stationary frame.
The EVENT that is the origin, in space AND TIME, is fixed and cannot be moving BECAUSE it is a point in time, and movement is change of location over time!
But the ORIGIN of system K' the moving frame has to be changing location over time, BECAUSE it is moving!

My apologies for sending the train through space!

 

[Dale]

And that is EXACTLY what I said! The location of frame K', its origin will be moving in system K'. BECAUSE IT IS A MOVING FRAME in system K, the stationary frame.
The EVENT that is the origin, in space AND TIME, is fixed and cannot be moving BECAUSE it is a point in time, and movement is change of location over time!
But the ORIGIN of system K' the moving frame has to be changing location over time, BECAUSE it is moving!

My apologies for sending the train through space!

It is important to learn and use correct terminology. The origin of any frame is defined as the event (0,0,0,0). All frames agree on the coordinates of that event in the standard configuration (by design). The origin of any frame never moves.

The thing that you are occasionally referring to as the origin and claiming that it moves is not the origin. The correct word is the "time axis". In the unprimed frame the unprimed frame's time axis is $(t,x,y,z)=(\tau,0,0,0)$. You can easily use this to calculate the line of the unprimed time axis in the primed frame as a function of $\tau$.

Please use the correct terminology now that it has been explained to you. If you find yourself resorting to all caps it is probably a sign that someone is using incorrect terminology.

 

[Ibix]

In other words, you are mixing three and four dimensional thinking again. Or at least three andafour dimensional terminology.

 

[Ibix]

Here is a sequence of still images of a car passing by a tree, accompanied by close-ups of a clock that is stationary with respect to the tree. Note that time is increasing up the page, and that the car passes the tree (call this x=0) at time t=0.

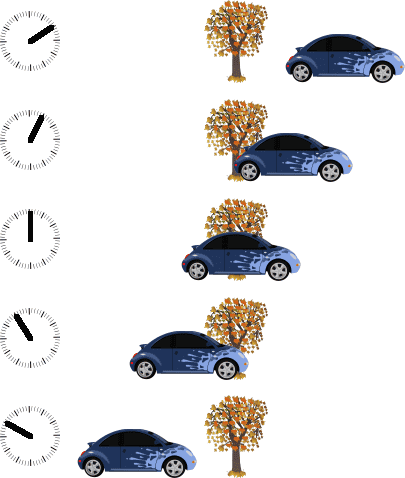
Here is the same sequence of images viewed from the frame in which the car is at rest, with close-ups of the car's dashboard clock. Again, time is increasing up the page. In this frame it is the tree passing the car - again we call this x'=0 and note that t'=0.

I think that you are still confusing points and events, and that is making you confused about what the Lorentz transforms are doing. The tree and the car are both points (or, at least, their centers of mass are points). In the top picture, the car is moving but the tree is not. A point that is not moving appears in the same place in every picture. A point that is moving appears at a different place in each picture.

In contrast, an event (for example, the origin (t,x,y,z)=(0,0,0,0), where and when the car and tree pass each other) only appears in one picture. It is a point at a specific time. You keep insisting that events do not move; I would say that events neither move nor are stationary. Motion is change of position with time, and since events don't exist for any length of time, they cannot be said to be moving or stationary. They only exist at one instant, so velocity is not defined for them.

The origin of spatial coordinates - (x,y,z)=(0,0,0) - is a point, and it could be stationary or moving. For example, the origin of spatial coordinates in my second diagram is the location of the car, and you can clearly see that it is a moving point in the first diagram. However, this is not the origin for the frame in a 4d sense - that is the event when the car and tree pass (t,x,y,z)=(0,0,0,0). You are confusing the origin of spatial coordinates with the origin of space-time coordinates. The first can be moving, but is not what we mean by "origin" when we're talking about Lorentz transforms. The origin, in this context, is the origin of space-time coordinates, which is the event (0,0,0,0), which appears only in the middle image in each diagram. It is neither moving nor stationary since it is a position at an instant, and velocity cannot be defined in an instant.

The Lorentz transforms simple relate the positions and times of events measured in one frame to the positions and times measured in another. You've done some examples. The diagram below may help - it shows a grid of (x,t) coordinates in black and a grid of (x',t') coordinates in red, for the case where the primed frame is moving at 0.6c. If you know the coordinates of an event on the black grid, the Lorentz transforms simply tell you the coordinates on the red grid without you having to go out and measure them, too.

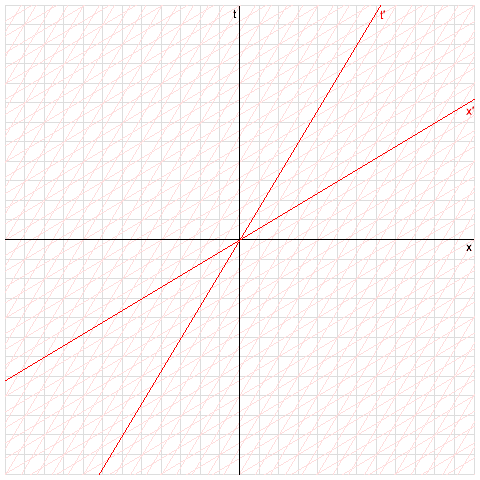
Hope all that was helpful.

 

[Dale]

I would say that events neither move nor are stationary. Motion is change of position with time, and since events don't exist for any length of time, they cannot be said to be moving or stationary. They only exist at one instant, so velocity is not defined for them.

Well said. Terms like "fixed" seem to imply that it has a well defined velocity and that velocity is equal to 0. But that isn't correct.

 

[Ibix]

Just to clarify something about the last diagram in my last post. In both the red and black frames, the origin of coordinates is the point where the axes cross - i.e. (x,t)=(0,0) or, equivalently, (x',t')=(0,0). The origin of spatial coordinates, however, is the t or t' axis - the vertical black line an the steeper red line. Anything at rest in the red frame is moving in the black one.

Hopefully you can see the relationship between the Minkowski diagram and the first picture. If not, draw a black line through the trees and a red one through the cars.

 

[Grimble]

Thank you all once again; I stand corrected, I must admit I find it a bit of a trial getting the terms correct as my working life has been devoted to English rather than science and I think of an event as being fixed in time and space, i.e only existing at that one point.
I will try and be more precise in my terminology from now on.
Thank you once again for your patience.