Losing energy during Fast Fourier Transform

[Gordon89]

Alright guys.

First off, this is my first post (happy to be here!) and I'm hoping this is the correct section of the forum. I'm an engineering student, currently working towards finishing my master's thesis.

Short introduction. I am trying to simulate an ocean wave environment, as a superposition of simple traveling sinusoidal waves. The amplitudes and frequencies of these single components obviously is not random (this would hardly produce usable results), but are instead sampled from a standard Power Density Spectrum called a 'JONSWAP' spectrum. For an example, see http://www.wikiwaves.org/Ocean-Wave_Spectra (look for 'JONSWAP' on the page, approximately one screen down from the top).

The point being, that the wave climate I attempt generate is supposed to be statistically fully dependent on the input spectrum. The problem I have, is that when I attempt to analyse the resulting signal (a superposition of a few hundred sinusoids, with amplitude and frequency sampled from the PSD and phases randomly assigned between -pi and +pi) by Fast Fourier Transform, I expect to roughly get back my original PSD but I don't.

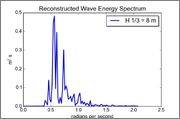
The shape of the resulting (reconstructed) spectrum looks quite nice but the amplitudes are off by a factor 30 or so (too low). Basically, I am loosing a heck of a lot of 'energy' somewhere between the sampling and FFS analysis. It is worth mentioning that analysis of the generated signal of sinusoids by using mathematical moments and some set relations between variables yields very good results, convincing me that the sampling of the amplitudes/frequencies and superposition parts function just fine.

The question to you guys being: what is happening here, and how can I accurately sample my generated signal?

I will freely admit that my knowledge of the FFT is not without gaps. Currently, I am sampling the signal and truncating the frequencies to be left only with the ones I am interested in (the ones from the original PSD). Then I plot the results. Please see the attached images.

Other information: working in Python (using the numpy FFT package).

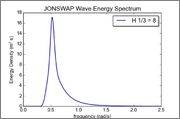
The original PDS:

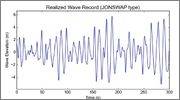
The signal constructed from it:

The reconstructed spectrum (note the much lower amplitudes):

Thanks for your input guys! Regards,Gordon.

 

[mfb]

Hard to tell if you do not show your calculations, but I would guess missing factors of 2 pi.

 

[Gordon89]

Thanks for the reply!

I guess showing you guys the calculations would have helped. I had been told that some inaccuracies are a natural part of the FFT, so I guess I was looking for a more phenomenological explanation.

As per usual however, it turned out the mistake was purely numerical - I forgot a small factor in the reconstruction process. After adding it, things look much better!