Lyapunov coefficient of Lorenz System

[carllacan]

Hi.

I'm trying to get the Lyapunov coeficient for a Lorenz System (namely, a laser, using the Lorenz-Haken model) but I'm not getting the plots that would be expected. This is how two trajectories with near identical initial conditions behave (only one of the variables):

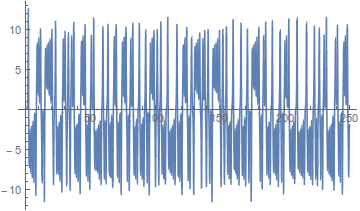
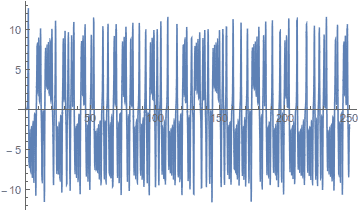
And here's the logarithm of the difference between the two (meaning the difference of the lengths of the vector in coordinate space):

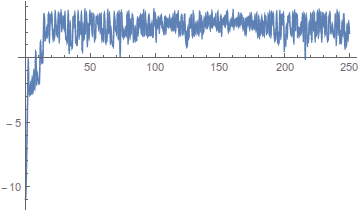
It looks like it grows exponentially at first, but then it stops. Why is this?

Here is my code (Mathematica):

t0 = 0;
tf = 250;

eps = 10^-5;

ecf = s (p[t] - f[t]);
ecp = -p[t] + d[t] f[t];
ecd = b (r - d[t] - f[t] p[t]);

par = {s -> 3., b -> 1, r -> 30};

solnum1 =
  NDSolve[{Derivative[1][f][t] == ecf, Derivative[1][p][t] == ecp,
     Derivative[1][d][t] == ecd, f[0] == 0.001, p[0] == 0.,
     d[0] == 1} /. par, {f, p, d}, {t, t0, tf},
   MaxSteps -> 10000000];
Plot[Evaluate[(f[t] /. solnum1), {t, t0, tf}], PlotRange -> All]

solnum2 =
  NDSolve[{Derivative[1][f][t] == ecf, Derivative[1][p][t] == ecp,
     Derivative[1][d][t] == ecd, f[0] == 0.001 + eps,
     p[0] == 0. + eps, d[0] == 1 + eps} /. par, {f, p, d}, {t, t0,
    tf}, MaxSteps -> 10000000];
Plot[Evaluate[(f[t] /. solnum2), {t, t0, tf}], PlotRange -> All]

Plot[Log[Sqrt[((f[t] /. solnum1) - (f[t] /. solnum2))^2 + ((p[t] /. solnum1) - (p[t] /. solnum2))^2 + ((d[t] /. solnum1) - (d[t] /. solnum2))^2]], {t, t0, tf},
PlotRange -> All]

 

[gtoguy97]

The Lyapunov coefficient should be calculated from the logarithm of the difference between the two trajectories, and it should be growing exponentially (at least for some time). Why is this not happening in my plot?