karush
Gold Member
MHB
- 3,240
- 5
$\tiny{M2215b.08}$
Find the volume of the solid
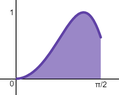
\begin{align*}\displaystyle y&=\sin (x^2)\\ 0&\le x \le \frac{\pi}{2}\\
\end{align*}
about the y-axis
View attachment 7629
ok this looks like a cylindrical Shell solution
So I set it up like this,,,,, hopefully
$\begin{align*}\displaystyle
V&=\int_0^12\pi x\left(\sin x^2\right)\ dx\\
\end{align*}$
Find the volume of the solid
\begin{align*}\displaystyle y&=\sin (x^2)\\ 0&\le x \le \frac{\pi}{2}\\
\end{align*}
about the y-axis
View attachment 7629
ok this looks like a cylindrical Shell solution
So I set it up like this,,,,, hopefully
$\begin{align*}\displaystyle
V&=\int_0^12\pi x\left(\sin x^2\right)\ dx\\
\end{align*}$