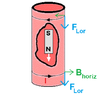
A falling neodymium magnet in a vertical copper pipe is decelerated due to Lenz's law, which generates induced currents that create an upward force counteracting gravity. The discussion raises questions about the behavior of free electrons in the copper, suggesting they should drift down with the magnet, yet they are held in place by electrostatic forces and resistive interactions. If the copper pipe had zero resistance, it could theoretically allow the magnet to fall indefinitely without deceleration, but this would contradict Newton's third law. The conversation also explores how the configuration of the conductor affects the terminal speed of the magnet, with suggestions for deriving a formula based on resistivity and other variables. Ultimately, the interaction between the magnet and the eddy currents is complex, involving both electromagnetic forces and the behavior of electrons within the conductive material.