- #1
Linus Pauling
- 190
- 0
1. What is the magnetic field at the center of the loop in the figure ?
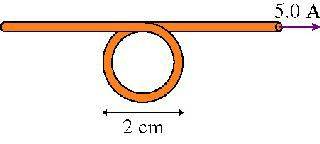
2. Ampere's Law
3. If the surface integral of B*ds = Bl = 2*pi*d = u0*I:
B = u0I / (2pi*d) = 5*5-5 T, which is wrong.
2. Ampere's Law
3. If the surface integral of B*ds = Bl = 2*pi*d = u0*I:
B = u0I / (2pi*d) = 5*5-5 T, which is wrong.