Magnetic field in a solenoid with rectangular cross-sectional area

[Hak]

Homework Statement

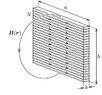
A solenoid of length $h$ has $N$ turns. The cross-section of the solenoid is a rectangle of sides $a$ and $b$, where $b \ll h \ll a$ (see the figure). Constant current $I$ flows in the coil wire. What is the shape of the magnetic field lines lying in the plane which is perpendicular to the sides $a$ and contains the geometrical center of the coil?

Relevant Equations

/

I was thinking of using magnetic monopoles, but I don't know how to do. I tried to calculate the magnetic flux through the cross section of the solenoid if a current $I$ flows through it. Magnetic induction inside can be given as $B = \mu_0 n I$, whereas magnetic induction at a distance $x$ form axis is $B = \mu_0 \frac{N}{2 \pi x} I$. So, magnetic flux through elemental strip is $d\Phi = B h dx$. Total flux the cross section is $\Phi = \int d\Phi = \int\frac{\mu_0 NI}{2 \pi x} h dx.$ How to continue? Do you have any hints?

 

[erobz]

?

It's not recommended to do this "thread bumping"... the moderators don't like it. Someone will get to your question when they can.

 

[Hak]

Ok, thank you for information. May I ask if you have any tips?

 

[erobz]

Ok, thank you for information. May I ask if you have any tips?

Sorry, not in this area.

 

[Hak]

Sorry, not in this area.

I don't think I understood.

 

[erobz]

I don't think I understood.

I mean I haven't given thought to electricity/magnetism in this type of theoretical treatment in over 15 years. Mechanical Engineer...not Physicist.

 

[Hak]

I mean I haven't given thought to electricity/magnetism in this type of theoretical treatment in over 15 years. Mechanical Engineer...not Physicist.

I'm sorry, I couldn't have known. I still thank you for the information.

 

[BvU]

I was thinking of using magnetic monopoles

magnetic monopoles are the equivalent of single electric charges in electrostatics. Is that really useful here ?

with $b << h << a$, do you see an analogy with another electrostatic case ?$\$

 

[Hak]

magnetic monopoles are the equivalent of single electric charges in electrostatics. Is that really useful here ?View attachment 331793

with $b << h << a$, do you see an analogy with another electrostatic case ?$\$

The field lines will be circular. Think of it as a uniformly magnetized block similar to electrically polarised block and hence there will be surface bound charge densities of opposite polarity at both faces. Due to this, the faces will behave as wires having opposite charge densities and so the field lines will be uniform and straight inside and for outer points it will behave as a point dipole (since $h \ll a$).
I think it is quite difficult to set up an analytical approach, although I think it is necessary (otherwise the text would not provide all this data, in my opinion). Would you have any hints on this?

 

[BvU]

I wouldn't expect the exercise requires an explicit expression. 'What is the shape of the magnetic field lines' ??
$b << h << a$ to the extreme (e.g. 0, 1, $\infty$) would already be very awkward. Two sheets of current ?

(In the picture I see $h \approx a$, not $h<<a$ )

$\$

 

[Hak]

I wouldn't expect the exercise requires an explicit expression. 'What is the shape of the magnetic field lines' ??
$b << h << a$ to the extreme (e.g. 0, 1, $\infty$) would already be very awkward. Two sheets of current ?

(In the picture I see $h \approx a$, not $h<<a$ )

$\$

I have no idea. Your observations are well-founded, but then why all this data? More importantly, why these discrepancies? This problem does not convince me and I do not like it. If you come up with any other ideas or if you would like to make any other suggestions, I would appreciate any further input.

 

[BvU]

I don't have any good ideas here; perhaps @haruspex ?

$\$

 

[haruspex]

I first considered one turn of the wire. The algebra is similar to that for a dipole. I got that at $(x,y)$ relative to the turn the field is proportional to $(\frac{2bxy}{r^4}, \frac b{r^2}(\frac{2x^2}{r^2}-1))$.
Then I integrated in the y direction, taking the origin at the centre of the solenoid. I assumed $r>>h$, which may or may not be the intent.
I got $(\frac{2bhxy}{r^4},\frac{bh}{r^2}(\frac{2y^2}{r^2}-1))$.
Haven't tried to figure out what the field lines look like.

 

[Hak]

I first considered one turn of the wire. The algebra is similar to that for a dipole. I got that at $(x,y)$ relative to the turn the field is proportional to $(\frac{2bxy}{r^4}, \frac b{r^2}(\frac{2x^2}{r^2}-1))$.
Then I integrated in the y direction, taking the origin at the centre of the solenoid. I assumed $r>>h$, which may or may not be the intent.
I got $(\frac{2bhxy}{r^4},\frac{bh}{r^2}(\frac{2y^2}{r^2}-1))$.
Haven't tried to figure out what the field lines look like.

May I ask how you performed the calculations? How do you think this could be traced back to the shape of the (presumably circular) magnetic field lines?

 

[haruspex]

May I ask how you performed the calculations? How do you think this could be traced back to the shape of the (presumably circular) magnetic field lines?

First, figure out the field at $(x,y)$ due to an infinite wire normal to the XY plane at $(b/2,0)$. Do the same for the current in the opposite direction at $(-b/2,0)$, add them up and take a first order approximation for small b.
Post what you get.

Having found the field in general as $(f_x(x,y),f_y(x,y))$, the field line would be the solution of $\frac{dy}{dx}=\frac{f_y}{f_x}$.

 

[Hak]

First, figure out the field at $(x,y)$ due to an infinite wire normal to the XY plane at $(b/2,0)$. Do the same for the current in the opposite direction at $(-b/2,0)$, add them up and take a first order approximation for small b.
Post what you get.

Having found the field in general as $(f_x(x,y),f_y(x,y))$, the field line would be the solution of $\frac{dy}{dx}=\frac{f_y}{f_x}$.

Is what you have advised me in this message to be considered in correlation with the previous message, or is the latter to be abandoned and one must start afresh?

 

[haruspex]

Is what you have advised me in this message to be considered in correlation with the previous message, or is the latter to be abandoned and one must start afresh?

The first paragraph in post #15 is an outline of how I arrived at the expressions in post #13.

 

[Hak]

Thank you very much. I meant to ask you whether the second expression in post #13 is related to the second paragraph in post #15 or not. Before doing the calculations, I would like to know whether or not you have thought of a method to find the field in general such as $(f_x (x,y), f_y (x, y))$.

 

[haruspex]

Thank you very much. I meant to ask you whether the second expression in post #13 is related to the second paragraph in post #15 or not. Before doing the calculations, I would like to know whether or not you have thought of a method to find the field in general such as $(f_x (x,y), f_y (x, y))$.

Post #13 gives the expressions I found for $f_x, f_y$, (but as I noted, I made the approximation $r>>h$, which is certainly not true inside the solenoid, so this might not be good enough). Where it is ok, you can plug them into the equation in post #15 and try to solve the differential equation.

 

[Hak]

Thank you once again. You are right, for $r \gg a$ may not fit that equation, but how to do it for $h \ll a$? However, I will take your advice and try to solve the differential equation anyway.

 

[Hak]

I solved the differential equation with your expression for $f_x, f_y$, finding:

$$y(x) = - \frac{\sqrt{r^2 - C_1 x^2}}{\sqrt{2}}$$ and $$y(x) = \frac{\sqrt{r^2 - C_1 x^2}}{\sqrt{2}}$$. So? Is it correct? What should I do now?

 

[haruspex]

I solved the differential equation with your expression for $f_x, f_y$, finding:

$$y(x) = - \frac{\sqrt{r^2 - C_1 x^2}}{\sqrt{2}}$$ and $$y(x) = \frac{\sqrt{r^2 - C_1 x^2}}{\sqrt{2}}$$. So? Is it correct? What should I do now?

Are you sure you did that right? Remember, r is a variable here. You must substitute $r^2=x^2+y^2$ before solving the ODE.

 

[Hak]

Are you sure you did that right? Remember, r is a variable here. You must substitute $r^2=x^2+y^2$ before solving the ODE.

You are right, I was wrong. I redid the calculations, arriving at the result:
$$y(x) = - \sqrt{C_1 x - x^2}$$ and $$y(x) = \sqrt{C_1 x - x^2}$$. So?

 

[haruspex]

You are right, I was wrong. I redid the calculations, arriving at the result:
$$y(x) = - \sqrt{C_1 x - x^2}$$ and $$y(x) = \sqrt{C_1 x - x^2}$$. So?

That is a very well known shape! Perhaps too simple because of my approximation?
See if you can do the y-integration in post #13 without assuming $r>>h$. (Note the correction; $r>>h$, not $r>>a$.)

 

[Hak]

That is a very well known shape! Perhaps too simple because of my approximation?
See if you can do the y-integration in post #13 without assuming $r>>h$. (Note the correction; $r>>h$, not $r>>a$.)

Circular shape should be the correct answer. But how to be able to prove the same for $h \ll a$? I do not know how to do the y-integration in post #13 without assuming $r>>h$. If you have any ideas, could you let me know so I can try to do this integration? @haruspex

 

[haruspex]

Circular shape should be the correct answer. But how to be able to prove the same for $h \ll a$? I do not know how to do the y-integration in post #13 without assuming $r>>h$. If you have any ideas, could you let me know so I can try to do this integration? @haruspex

Please post your attempt at the integration.