Magnetic field of a finite wire increasing with distance?

[MrManhattan]

I am computing magnetic field around a thick conductor to do railgun force modeling. I am currently re-examining my magnetic field computation, and I have found some confusing results stemming from a fairly simple use of the Biot-Savart Law. The main issue is that the more nuanced application of Biot-Savart gives a magnetic field that increases as distance from the wire increases. This doesn't make sense to me.

I am following these papers: MIT ILR Lizhong

Everything I'm doing now stems from the following equation (9.1.5 in the MIT reference)

B = μ₀ * I / (4 * π * r) * ( cos(θ₂) + cos(θ₁) )

for the more simple case where θ₂ goes to 90° this simplifies to:

B = μ₀ * I / (4 * π * r) * l / √(l² + r²)

shown as equation 1 in the ILR reference. Considering this equation in 3D yields the following from equation 2 of the Lizhong reference:

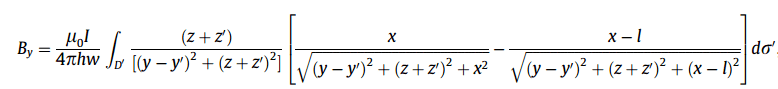
where the coordinates are defined as follows:

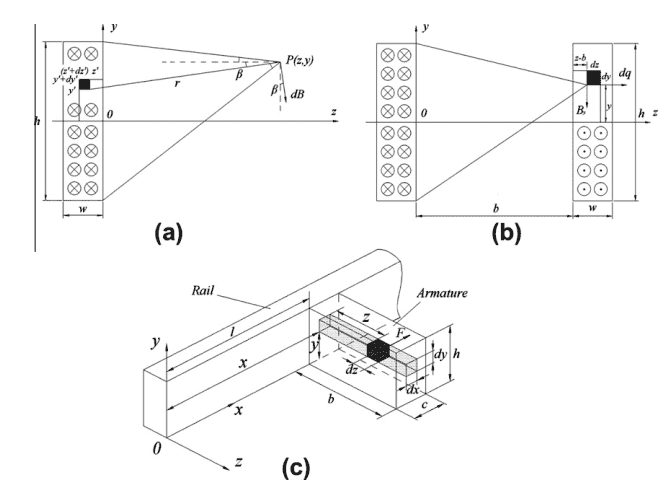For this application, I am looking at the points near (at and past) the end of a straight wire as shown below.

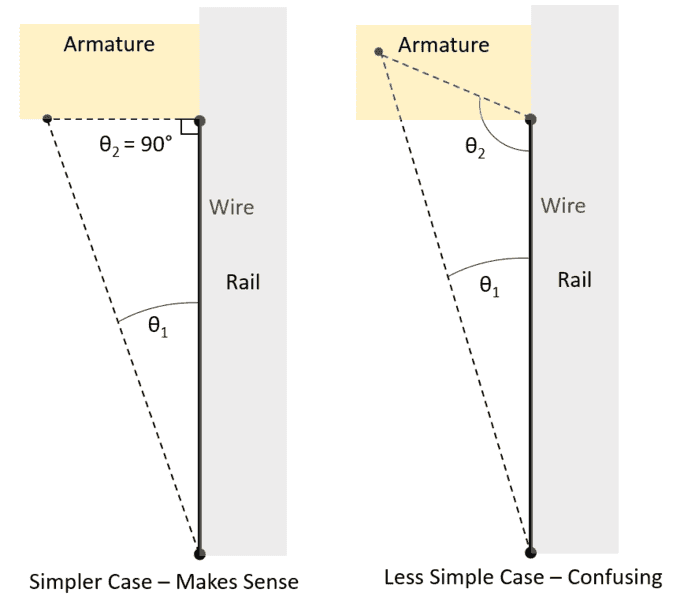
When I compute the magnetic field about a finite wire assuming the point is at the end of the wire (θ₂ = 90° as shown on the left) I get seemingly reasonable results by approximating magnetic field "deeper" into the armature (further away from the end of the wire) by simply changing r to the following:

r = √( z² + y² + (x-l)² )

This gives me the following graph, where the surfaces represent the magnetic field at the various thickness ("depth") sections of the armature. The z axis is the magnetic field strength, and the other two axes are the width and height of the armature (where height would be into the page in the previous figure).

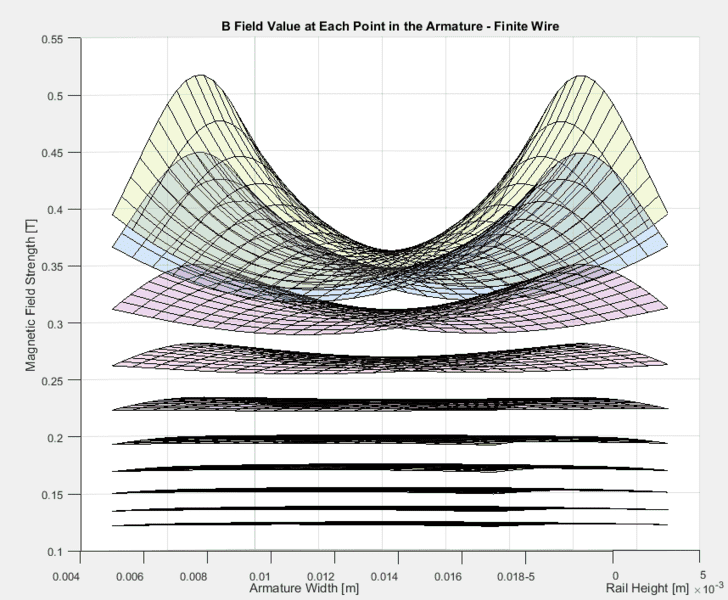
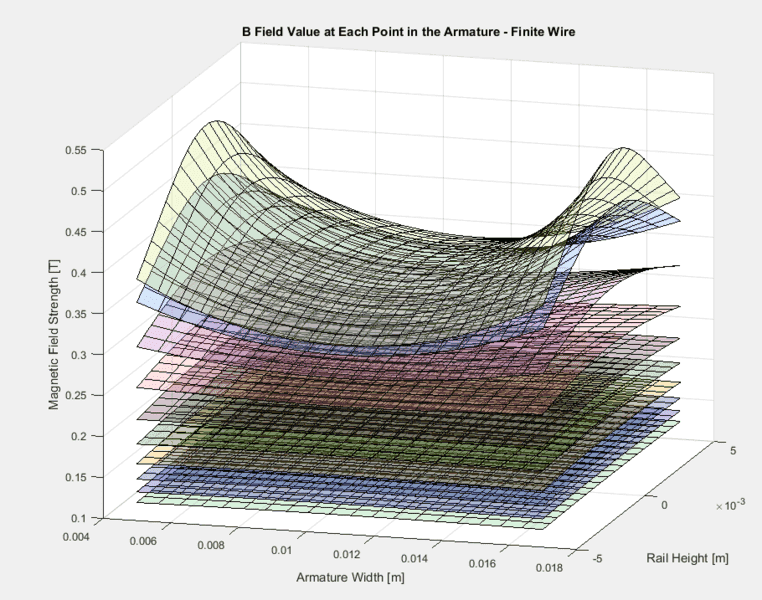
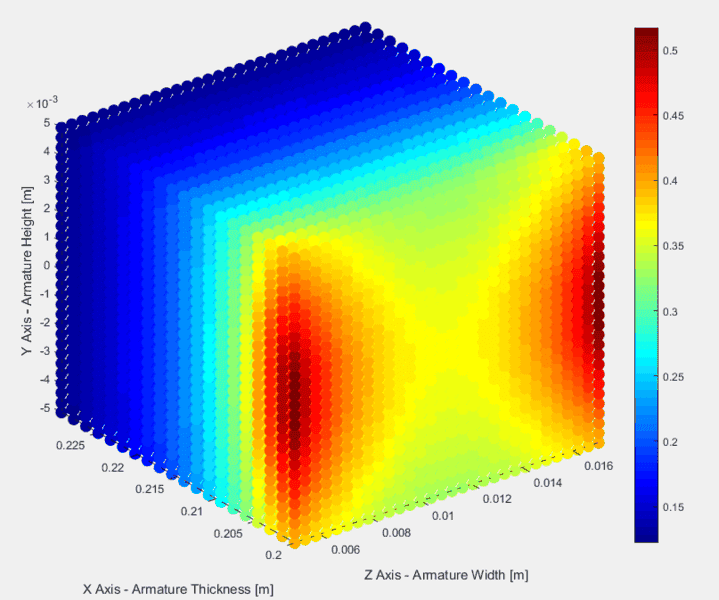
I say these results seem reasonable because the shape of the magnetic field is maintained as the distance from the current carrying "wire" increases. The field is smaller near the top and bottom of the rail (further from the wire) and near the center of the two rails (further from both "wires").

However, when I use the full equation from the Lizhong paper (which I was also able to derive myself just using trig) I get the following:

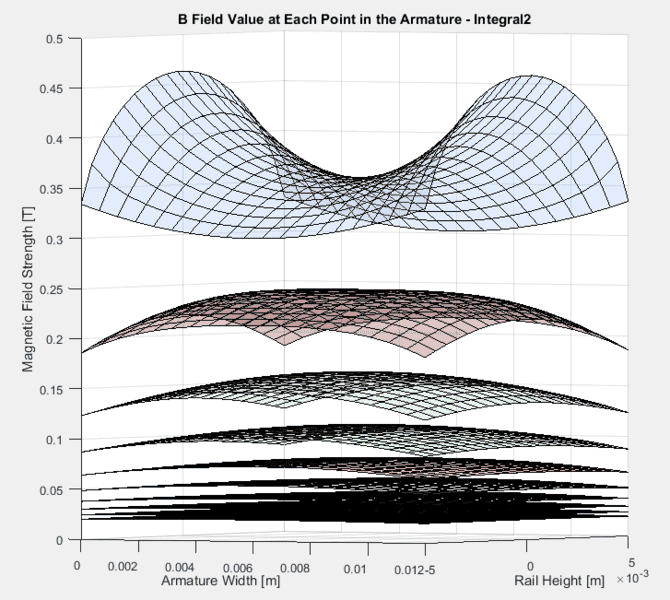
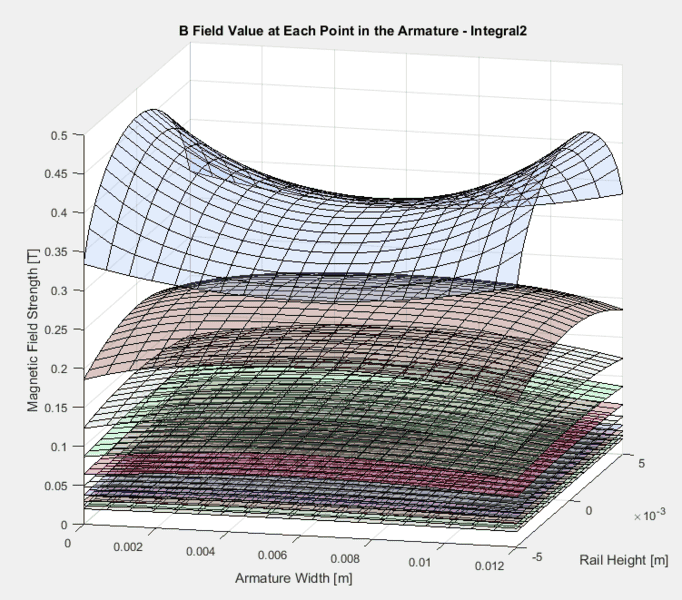
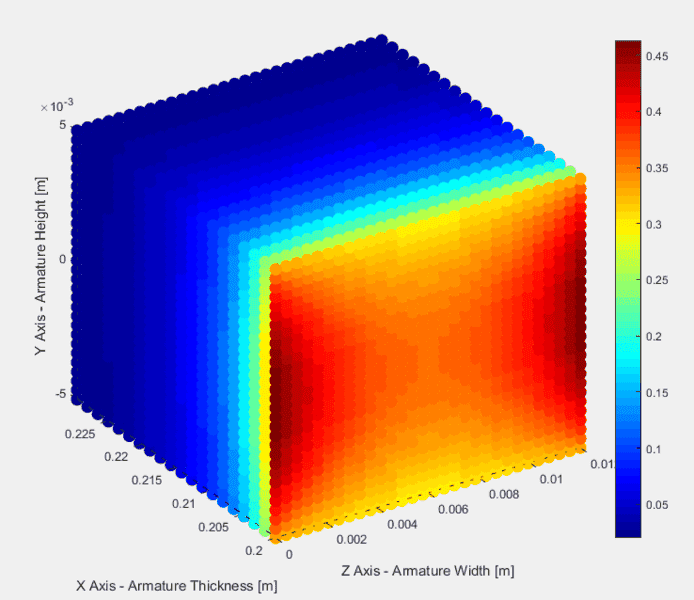
These don't seem to make sense because, other than the rear face, the magnetic field is LARGER in the middle of the two rails, than at the edge, right next to the wire. I can understand that the field will fall off faster in the wire length direction, as there's no longer any wire supporting the field. But that shouldn't mean that the field at a point, say 2 mm away in the length direction and 1 mm away in the other two directions has a smaller B field value than a point 2 mm away in the length direction and 3 mm away in the other two directions.

I see how this comes about in the math. The second term of the Lizhong equation 2 is only nonzero when looking at position that has some depth into the armature (distance past the wire end). This term gets smaller and smaller as distance increases in the other two directions. So, if you're subtracting smaller values, your result will end up being larger, giving me the result of higher magnetic field further away from the wire.

Is this physically accurate? Does it have something to do with the field wrapping around the end of the wire?

 

[mfb]

The magnetic field behind the end of the wire has to be continuous - it has to go to zero if you approach the wire axis. As it is non-zero elsewhere, it increases with distance (from the axis) up to some maximal distance, then it decreases again. This maximal distance should be proportional to the distance behind the end of the wire considered.

You can also see this in the original Biot-Savart law:
$$\mathbf{B}(\mathbf{r}) = \frac{I \mu_0}{4\pi} \int \frac{d\mathbf l\times\mathbf{r'}}{|\mathbf{r'}|^3}$$

For $\theta_2 \approx \pi$, the absolute value of r' does not depend notably on the separation from the wire (in the integration range), but the numerator is proportional to this separation due to the different angle. Therefore, the magnetic field strength is proportional to the distance from the wire axis for small distances.